吓哭了。

计数 DP 通常解决方案数统计问题，如求满足条件的集合 $S$ 的数量，直接枚举会达到指数复杂度，可以通过一些计数方法降低时间复杂度。此类问题状态的设计，关键在于 不重不漏。

CF559C Gerald and Giant Chess

$H\times W$ 的棋盘上有 $n$ 个黑棋，从 $(1,1)$ 出发，到 $(H,W)$ 结束。求不经过黑棋的方案数。$H,W\le 10^5$，$n\le 2000$。

如果不考虑黑棋，总方案为 $\dbinom{H+W-2}{W-1}$。如果减去所有经过黑棋的方案，那么就是答案了。且黑棋较少，故考虑设计有关 黑棋 的状态。

设 $f_i$ 表示到达第 $i$ 只黑棋，不走其他黑棋的方案数。由于路径只能向下与向右，因此只有第 $i$ 只棋 左上方 的棋会影响当前结果。所以，我们依次枚举其所有右上角的黑棋，并减去相应的路径数。那我们不妨先从左到右、从上到下给棋子排序。在统计答案时，我们无需考虑是否会经过多个黑棋。我们观察答案形式：$\dbinom{X_i+Y_i-2}{X_i-1}-C_1-C_2-\cdots-C_{i-1}$，其中 $C_j$ 表示从起点到棋子 $i$ 经过 $j$ 只黑棋的路径数（不包括 $i$）。我们的答案是：$f_i=\dbinom{X_i+Y_i-2}{X_i-1}-\sum f_j\times {{X_i-X_j+Y_i-Y_j}\choose{X_i-X_j}}$。实际上，对于每个 $j$，后项的含义为 以棋子 $j$ 为起点 到达棋子 $i$ 的路径总数，实际上统计了所有 $(X_j,Y_j)\to(X_i,Y_i)$ 走过任意黑棋的方案数，因此路径方案与上式是 一一对应 的。

我们不妨假设第 $0$ 只黑棋为 $(0,0)$，第 $n+1$ 只棋子为 $(H,W)$，那么答案即为 $f_{n+1}$。

实际上，通过这道题目，我们得到计数 DP 状态设计的重要一点，即「互斥性」。一个状态被划分成若干个子问题不应有重叠，才能不重不漏地统计方案。

CF1227F2 Wrong Answer on test 233 (Hard Version)

做一步容斥：相当于全体序列减去移动后答案不变的序列总数的一半，也就是 $\dfrac{k^n-ians}2$。考虑如何计算这个 $ians$。

为什么是一半？

因为移动序列后可能减少也有可能增加。

我们发现减少其实是增加的逆过程，

右移增加对应着左移减少，因此这两个过程是对称的。

对于 $h_i=h_{(i\bmod n)+1}$ 的所有 $i$，显然可以随便填，假设有 $p$ 个这种位置，那么给答案的贡献是 $k^p$。

接下来考虑 $h_i\not=h_{(i\bmod n)+1}$ 的所有 $i$，这种 $i$ 共有 $q=p-i$ 种。假设其中有 $m$ 个位置使移动后答案增加，那么根据对称性，必然有 $m$ 个位置在移动后使答案减少。这一部分的贡献是 $\dbinom{q}{m}\dbinom{q-m}{m}$，即在剩余 $q$ 个位置中选增加与减少的，这些值是由 $h$ 确定的。那么剩下的就是不变的，这些值除了 $h_i$ 和 $h_{i\bmod n+1}$ 不可选外，其余均可选。由于 $h_i=h_{i\bmod n+1}$ 的情况已经考虑，因此有 $k-2$ 种选法。

那么 $ians=k^{p}\sum\limits_{m=0}^{\lfloor \frac q2\rfloor}\dbinom{q}{m}\dbinom{q-m}{m}(k-2)^{q-2m}$，答案即为 $\dfrac{k^n-k^{p}\sum\limits_{m=0}^{\lfloor \frac q2\rfloor}\dbinom{q}{m}\dbinom{q-m}{m}(k-2)^{q-2m}}2$。时间复杂度 $\mathcal O(n\log n)$。

排列计数

相对排名法

Reference: 浅谈一类带限制的排列计数问题 大概是给出排列的相对排名，然后要你求方案数。

我们发现这其实可以划分成多个子问题，子问题之内又是一个新的问题。甚至可以继承。

Permutation

一句话题意：给出排列相邻元素的大小关系，求满足条件的排列数，$n\le 3000$。

如果将一段单独拿出，可以发现这是一个新的子问题，因此考虑合并这些子问题。

用从左往右的顺序来合并。设 $f(i,j)$ 为考虑了前 $i$ 个元素，第 $i$ 个元素在这其中的排名为 $j$ 的方Ciallo～(∠・ω< )⌒★案数。有转移式：

$$f(i,j)=\begin{cases}\sum\limits_{k<j}f(i-1,k),&a_{i-1}=\texttt{<}\\sum\limits_{k\ge j}f(i-1,k),&a_{i-1}=\texttt{>}\end{cases}$$

$f(1,1)=1$。前缀和优化即可做到 $\mathcal O(n^2)$。

Girl Permutation

单独把前后缀最大值提出来，发现是一个先递增，达到最值 $n$ 后递减的山峰状。

显然的，$a(p_{m_1})=a(s_1)=n$，我们就可以将整个排列独立地分成左右两部分，并给左右两边分配数值，也就是 $\dbinom{n-1}{p_{m_1}-1}$ 种方案。作为独立的一部分，自然可以看作一个新排列的答案。接下来讨论左边的情况。

独立地看左边，显然这是一个简化后的原问题：只不过最大值右侧可以随意填。设前缀最大值 $[1,i]$ 的答案为 $f(i)$，那么 $f(p_{m_i})=f(p_{m_{i-1}})\times\dbinom{p_{m_{i+1}}-2}{p_{m_{i+1}}-p_{m_i}-1}\times(p_{m_{i+1}}-p_{m_{i}}-1)!)$。特别的，$f(1)=1$。

对于右边也是类似的，也可以将序列与索引反转做一遍上述过程，假设后缀最大值 $[i,n]$ 的答案为 $g(i)$。则答案为 $f(p_{m_1})g(s_1)\dbinom{n-1}{p_{m_1}-1}$。

处理排列问题的通常思路，也就是将其划分成多个独立排列，划分成简单的子问题。

Similar Permutation

和例题差不多，设 $f(i,k,p,q)$ 表示前 $i$ 个元素，$A_i$ 的排名为 $p$，$B_i$ 的排名为 $q$，有 $k$ 个元素满足限制的方案。

CF995F Cowmpany Cowmpensation

这个 $D$ 很大，但是想一想就会发现，这其实没什么用。可以求出相对排名之后将 $D$ 个元素映射到不同的答案上去。

设 $f(u,k)$ 为以 $u$ 为根的子树中，$a_u$ 为第 $k$ 小的数的方案数。那么有转移式：

$$f(u,k)=\prod\limits_{v\in son_u}\sum\limits_{p\le k}f(v,p)$$

然后前缀和优化一下，就是：

$$f(u,k)=\prod\limits_{v\in son_u}s(v,k)$$

小 Tip：为什么不设成第 $k$ 大呢？因为我们最终统计结果必然是从根来看，如果使用第 $k$ 大，根必然是第 $1$ 大。没有体现实际上树内结构中的不同元素总和。

这算的实际上是“至多有 $k$ 个不同元素”，考虑二项式反演： $$f(1,j)=\sum\limits_{k\le j}\dbinom{j-1}{k-1}g(1,k)\iff g(1,j)=\sum\limits_{k\le j} (-1)^{k+j}\dbinom{j-1}{k-1}f(1,k)$$

为什么是 $\dbinom{j-1}{k-1}$？ 因为已经固定必选 $j$ 了。

我们要求的是每个 $g(1,j)$，因此用反演和移项就可以以相同的复杂度递推出 $g(1,k)$：

$$$$

答案就是 $\sum\limits_{k\in[1,n]}\dbinom{D}{k}g(1,k)$

P4099 [HEOI2013] SAO

给出一个弱连通含有 $n-1$ 条边的 $n$ 个节点的图，一条边表示了先后顺序。对所有满足给出顺序的拓扑序计数。$n\le 1000$。

实际上就是一棵树。

设 $f(u,i)$ 表示在 $\operatorname{subtree}(u)$ 中，$u$ 的排名为 $i$ 的方案数。假设 $v\in \operatorname{subtree}(u)$ 且 $v$ 在 $u$ 之前。考虑 $v$ 子树内有多少个点插在 $u$ 的前面，设为 $k$ 个。那么也就是先在 $i$ 之前的 $i$ 个缝隙中放 $k$ 个数，再在 $i$ 之后的 $siz_u-i+1$ 的缝隙中放入 $siz_v-k$ 个数。根据插板法，有 $\dbinom{k+i-1}{i-1}\dbinom{siz_v-k+siz_u-i}{siz-i}$ 种方案，再将两种方案合并，就有转移式：

$$f(u,i+k)=\sum\limits_{k\ge j} f(u,i)\cdot f(v,j)\cdot\dbinom{k+i-1}{i-1}\cdot\dbinom{siz_v-k+siz_u-i}{siz-i}$$

注意到这个东西就是

$$f(u,i+k)= f(u,i)\dbinom{k+i-1}{i-1}\dbinom{siz_v-k+siz_u-i}{siz-i}\sum\limits_{j\le k}f(v,j)$$

前缀和优化，就做完了。

连续段 DP

Reference: 浅谈一类处理状态转移依赖邻项的排列计数问题的 dp 策略：连续段 dp（线头 dp）

这个 DP Trick 通常用于处理状态相邻的一种排列计数问题。由于转移只和相邻的状态有关，因此只需要记录连续段的数量，以及插入时的分类讨论。

通常，连续段 DP 的状态设计为：$f(i,j)$ 表示前 $i$ 个元素，形成了 $j$ 个连续段的方案数。对于新元素 $i$，转移有如下的讨论：

1. 新建连续段
2. 合并连续段
3. 将 $i$ 放在某个已有的连续段内。

Phoenix and Computers

我们把连续打开的电脑视作一个连续段。

我们可以如法炮制地进行状态设计以及讨论：$f(i,j)$ 表示前 $i$ 台电脑形成了 $j$ 个连续段的方案数。

考虑当前如何插入一个元素。

• 新增连续段。
  • 从 $f(i-1,j-1)$ 转移而来，$j-1$ 个连续段有 $j$ 个空隙，于是有 $f(i,j)\gets f(i-1,j-1)\times j$。
• 合并连续段
  • $j$ 个连续段中有 $j-1$ 个空隙两边都有连续段。考虑中间有几个空位：
    • $2$ 个空位。那么在两个位置中任选一个，打开电脑即可，另一个位置会自动打开。
    • $3$ 个空位。只有放在中间才能一次实现合并。
  • 因而，有转移：$f(i,j)\gets f(i-3,j+1)\times j$ 以及 $f(i,j)\gets f(i-2,j+1)\times 2\times j$。
• 放在某个连续段之中。
  • 可以插在左右两侧：$f(i,j)\gets f(i-1,j)\times j\times 2$
  • 可以隔一个位置插入：$f(i,j)\gets f(i-2,j)\times j\times 2$

最终答案为 $f(n,1)$。

P5999 [CEOI 2016] kangaroo

一句话题意：求满足如下条件的所有排列：

• 对于所有 $i\in(1,n)$，$p_i>p_{i+1}$ 且 $p_i>p_{i-1}$ 或者 $p_i<p_{i-1}$ 且 $p_i<p_{i+1}$。
• $p_1=s$，$p_n=t$。

不难发现要求排列形如：…大小大小…

设 $f(i,j)$ 为插入了 $1\sim i$ 的所有数，有 $j$ 个连续段的方案数。由于当前的枚举顺序，当前插入的数必然比已经形成连续段的数都要大。对 $i$ 进行分类讨论：

• 新增连续段。虽然插入的 $i$ 是递增的，但首位与末尾是确定的。$f(i+1,j+1)\gets f(i,j)\times (j+1-[i>s]-[i>t])$。
• 合并连续段。$f(i+1,j+1)\gets f(i,j+1)\times j$
• 插入连续段两端。若可以插入，那么必然不满足条件，因此无这种情况。

P7967 [COCI 2021/2022 #2] Magneti

Reference 考虑一种磁铁排列，设第 $i$ 个磁铁的半径为 $s_i$（自减去 $1$）。那么要铺完这些磁铁，至少需要占 $S=\sum\limits\limits_{i\in[1,n-1]}\max(s_i,s_{i+1})$ 个空位。那么剩下的空位 $L-S-n$ 可以随便放。根据插板法，和为 $S$ 的排列的贡献为 $\dbinom{L-S-n+n}{n}=\dbinom{L-S}{n}$。

下面考虑如何计算这些排列。考虑连续段 DP，我们称这里的“连续段”为二者覆盖范围间没有空格（即“紧密相连”）。

设 $f(i,j,k)$ 表示放了前 $i$ 块磁铁，形成了 $j$ 个连续段，其 $S$ 和为 $k$ 的方案数。不妨使 $r_i$ 从小到大排序，这样统计答案会十分好做。进行分类讨论：

• 新增连续段：$f(i+1,j+1,k)\gets f(i,j,k)$。
• 合并连续段：$f(i+1,j-1,k+2r_i)\gets f(i,j,k)\times j\times (j-1)$
• 插入连续段两侧：$f(i+1,j,k+r_i)\gets f(i,j,k)\times 2\times j$

Permutation Oddness

P10547 [THUPC 2024 决赛] 排列游戏

1. Lemma. 一个排列 $p$ 变为 $p_i$ 的花费至少为 $\sum\limits_{i=1}^n \lvert p_i-i\rvert$。
2. 连 $p_i\to i$ 的边，一条边的贡献是 $\lvert p_i-i\rvert$。发现构成许多个环，且环内元素可以互相置换，

P2612 [ZJOI2012] 波浪

TBD.

P9197 [JOI Open 2016] 摩天大楼 / Skyscraper

TBD.

笛卡尔树

实际上和枚举最大值分治这类方法异曲同工。

.1 定义

笛卡尔树，是满足如下性质的数据结构：

1. 二叉树。
2. 权值中序遍历序列即原权值序列。
3. 满足大/小根堆性质。

下面这张图是很好的一个示例（图源维基百科）。

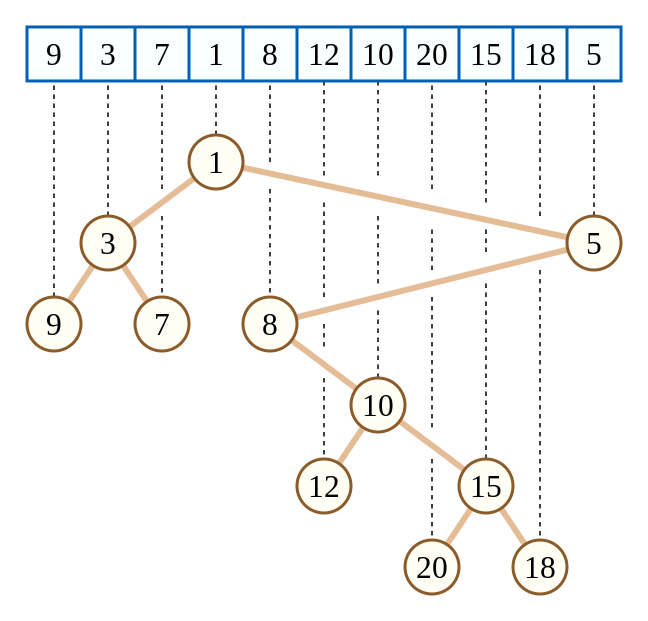
.2 构造过程

按照下标增长的顺序构建笛卡尔树，那么每次插入的新元素必然在当前节点的右链（所有节点均为右儿子的链）上。具体来说，我们用栈维护当前笛卡尔树的右链，栈顶是链底元素。对新增元素 $a_i$ 分类讨论：

• $a_i\ge a_{top}$，那么直接作为右儿子入栈即可。
• $a_i< a_{top}$，不符合性质。一直退栈直至为上一种情况。

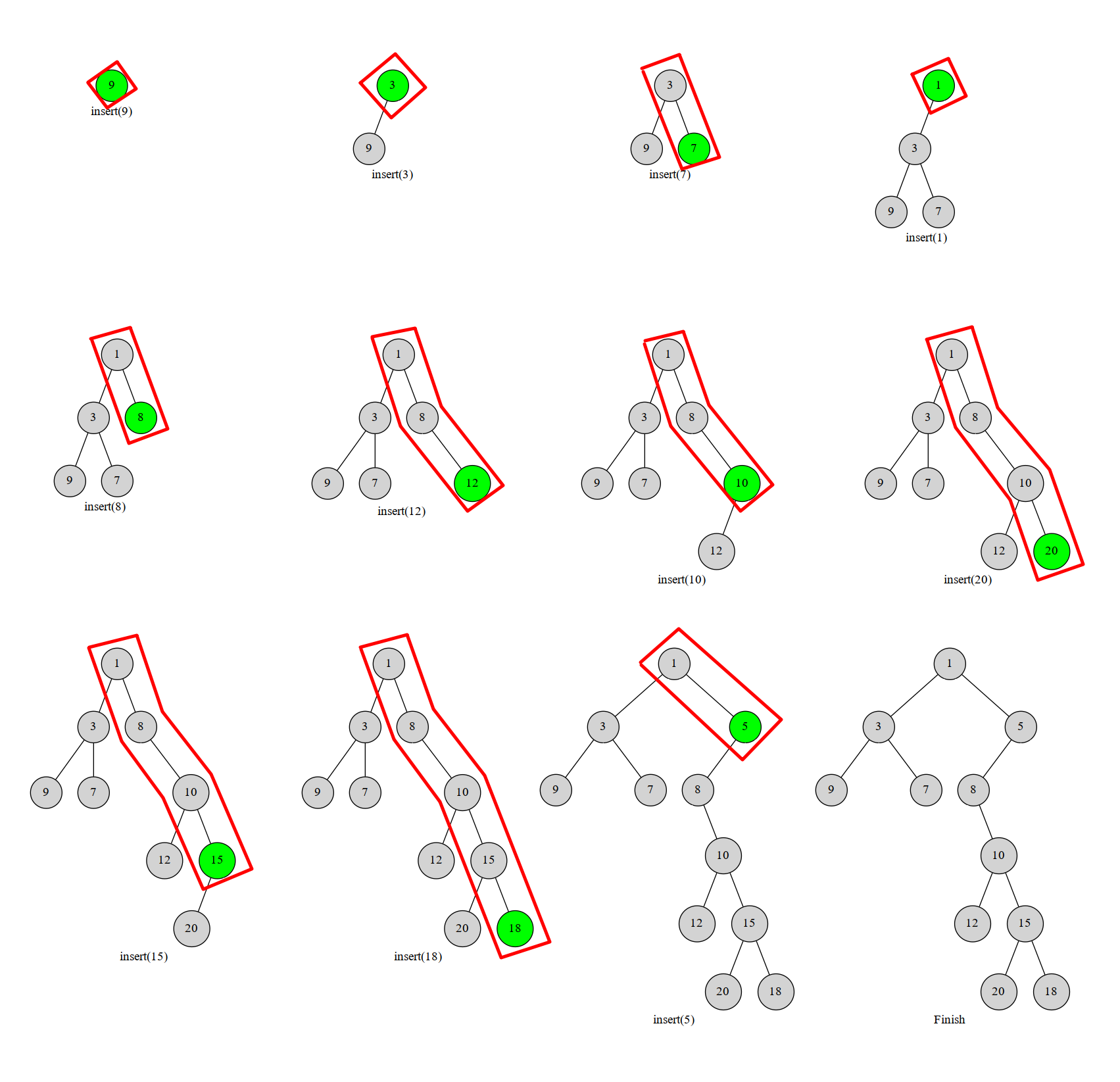
图源 OI-Wiki

构造的复杂度是 $\mathcal O(n)$ 的。

.3 例题

B4273 [蓝桥杯青少年组省赛 2023] 最大的矩形纸片

用小根堆的笛卡尔树对每个节点维护最长右链就做完了。

CF1748E Yet Another Array Counting Problem

一句话题意：求值域在 $[1,m]$ 内的与原序列任意一个子段最靠左边的最大值位置都相同的序列数量。

把这个东西转化到大根堆的笛卡尔树上，发现一段区间的「最左端最大值」就是 LCA，这道题也就是要求笛卡尔树形态相同。这也就是对值域在 $[1,m]$ 的笛卡尔进行计数。设 $f(i,j)$ 表示以 $i$ 为根的子树，$i$ 上填的数为 $j$ 的笛卡尔树的个数，那么：

$$f(u,w)=\sum\limits_{i=1}^{w-1}f(ls,i)\sum\limits_{i=1}^{w}f(rs,i)$$

前缀和优化一下，$f’(u,w)=f’(ls,w-1)\times f’(rs,w)+f’(u,w-1)$、

答案即为 $f’(rt,m)$。

P6453 [COCI 2008/2009 #4] PERIODNI

题意：给出连续的 $n$ 座山，每座山有高度 $h_i\le 10^6$。每一列，每一行（如果中间不断裂）只能填 $1$ 个数。求填 $k$ 个数的方案。

尝试将原图以水平线划分成多个矩形。那么自然会分层左右二部分，且层高递增，这让我们想到小根堆的笛卡尔树。具体而言，以 $h_i$ 为键值建笛卡尔树。设 $f_{u,w}$ 为以 $u$ 为根的子树，填了 $w$ 个数的方案。考虑层高为 $h_u-h_{fa_u}$，长度为 $siz_u$ 的矩形填数的方案数，这实际上是一个在 $n\times$ 的棋盘内放 $k$ 个互不攻击的「車」的问题。考虑选 $k$ 列，选 $k$ 行，任意排列。有转移：

$$f_{u,w}=\sum\limits_{i+j\le w}f_{ls,i}\cdot f_{rs,j}\cdot\dbinom{siz_u-i-j}{w-i-j}\cdot\dbinom{h_u-h_{fa_u}}{w-i-j}\cdot(w-i-j)!$$

对于 $i+j$，视作整体。令 $g_{u,w}=\sum\limits_{i+j\le w}f_{ls,i}\cdot f_{rs,j}$，那么 $f_{u,w}=\sum\limits_{w’\le w}g_{u,w’}\dbinom{siz_u-w’}{w-w’}\dbinom{h_u-h_{fa_u}}{w-w’}(w-w’)!$。

答案即为 $f_{rt,k}$。

P9084 [PA 2018] Skwarki

简要题意：求进行恰 $k$ 次操作，$n$ 阶排列仅剩下一个元素的排列个数：将所有比任一相邻元素小的元素删去。

可以确定的一点是，留下来的一定是最大值。假设这个最大值在中间，那么我们就可以将问题划分成左右两部分，且由于最大值的限制，这两部分相互独立。这就成功地将原问题划分成多个子问题，考虑如何转移。粗略来说，设 $f_{i,j}$ 表示 $i$ 个元素的排列，操作 $j$ 次删完的方案数。转移式大概是形如 $f_{i,j}=\sum\limits_{u}\dbinom{i-1}{u}f_{u,p}f_{i-1-u,q}$ 的形式。

进一步思考，发现 $f_{i,j}$ 是不完全的形式：我们在实际求解中其左右端点必有其一为父区间的全局最大值。因此新开一个维度，$f_{i,j,1/0}$ 表示 $i$ 个元素的排列，端点处有无全局最大值，操作 $j$ 次恰好删空的方案。

• 对于 $f_{i,j,0}$，左右端点必然都不是全局最大值，我们每次是从当前的区间最大值进行转移。

  • 若 $p\not=q$，由于左右端不是全局最大值，因此在一端删空之后，被父区间的其余元素删除，故此时 $j=\max(p,q)$。
  • 若 $p=q$，则两边同时被清空。需要在基础上再一次操作，即 $j=p+1$。

• 对于 $f_{i,j,1}$，不妨设 $p$ 为全局最大值所在处删完的次数（父区间不可能有两个全局最大值）。

  • 若 $p\le q+1$，那么就会被另一侧子树的父区间内删掉，$j=q+1$。
  • 若 $p>q+1$，那么会被区间最大值删掉，$j=p$。

综上所述，我们得到了一般的转移方程： $$f_{i,j,0}=\sum\limits_{p,q}\sum\limits_{u\in[1,i)}\dbinom{i-1}{u}f_{u,p,0}f_{i-1-u,q,0}$$ $$f_{i,j,1}=\sum\limits_{p,q}\sum\limits_{u\in[1,i)}\dbinom{i-1}{u}f_{u,p,1}f_{i-1-u,q,0}$$

我们只考虑一边的存在全局最值的情况，这是因为 $p,q$ 是对称的。

另外，每次删除的数量至少是序列的一半，即最多 $\log n$ 次就能删完。直接枚举的复杂度是 $\mathcal O(n^2\log^2n)$，前缀和优化后可以做到 $\mathcal O(n^2\log n)$。