组合数学

2025-08-21T13:54:42+08:00 | 23分钟阅读 | 更新于 2025-08-21T13:54:42+08:00

@ Jason Chan

最难了，我真的不会。

1. 排列组合

1.1 基本计数原理

1.1.1 加法原理

完成一件事有 $n$ 个方案，第 $i$ 中方案有 $a_i$ 个，那么总方案即为 $\sum a_i$。

1.1.2 乘法原理

完成一件事有 $n$ 个步骤，第 $i$ 个步骤有 $a_i$ 种方法，那么完成这件事的总方案为 $\prod a_i$。

实际上，在用这两个原理计算方案时，我们通常不会考虑这两件事。

1.2 排列数与组合数

1.2.1 排列数

从 $n$ 个不同数中任选 $m$ 个，形成有序排列的个数。记作 $A^m_n$。

根据乘法原理，有 $A_n^m=n\times (n-1)\times\cdots\times(n-m+1)=\frac{n!}{m!}=n^{\underline{m}}$。$n^{\underline m}$ 是 $n$ 的下降幂。

1.2.2 组合数

从 $n$ 个不同数中任选 $m$ 个，形成无序排列的个数。记作 $C^m_n$，也可记作 $n\choose m$。

实际上，组合数就是排列数去除排列后的结果。那么易得 ${n \choose m}=\frac{A^m_n}{m!}=\frac{n!}{(n-m)!m!}$。

1.2.3 多重组合数

是「多重集的排列数」的通常叫法，并非「多重集的组合数」！

组合意义是对于一个多重集（即拥有相同元素的集合，不妨设第 $i$ 种元素个数为 $n_i$）求全排列，全排列的个数，设 $N=\sum\limits_{i=1}^k n_i$，多重组合数表示为：

$$\dbinom{N}{n_1,n_2,\cdots,n_k}$$

考虑首先将所有元素视为不同，进行排列。再去掉相同元素排列的贡献，那么也就是：

$$\dbinom{N}{n_1,n_2,\cdots,n_k}=\dfrac{N!}{\prod\limits_{i=1}^k(n_i!)}$$

实际上，我们可以使用组合数来计算这个式子：

$$\dbinom{N}{n_1,n_2,\cdots,n_k}=\dbinom{N}{n_1}\times\dbinom{N-n_1}{n_2}\times\cdots\times\dbinom{N-\sum\limits_{i=1}^{k-1}n_i}{n_k}=\prod\limits_{i=1}^k\dbinom{N-\sum\limits_{j=1}^{i-1}}{n_i}$$

~~展开即证明，证明即展开。~~

1.3 组合技巧

1.3.1 二项式定理

$(a+b)^n=\sum\limits_{i=0}^n\dbinom ni a^ib^{n-i}$。

考虑展开式中共有 $n$ 个一次式相乘，相当于选 $i$ 个为 $a$，$n-i$ 个为 $b$，那么就是这个式子了。

特别的，$2^n=(1+1)^n=\sum\limits_{i=0}^n\dbinom ni$。

1.3.2 组合恒等式

$\dbinom{n}{m}=\dbinom{n}{n-m}$ 显然。
$\dbinom{n}{m}=\dfrac nm\dbinom{n-1}{m-1}$ 展开即可。
推论 1：$m\dbinom{n}{m}=n\dbinom{n-1}{m-1}$
推论 2：$(n-m)\dbinom{n}{m}=n\dbinom{r-1}k$
推论 3：$(n-m)\dbinom{n}{m}+m\dbinom{n}{m}=n\dbinom{n-1}{m-1}+n\dbinom{r-1}k$
递推式：$\dbinom nm=\dbinom{n-1}{m}+\dbinom{n-1}{m-1}$。

这个依然考虑组合意义：$n$ 选 $m$，有两种方式：在 $n-1$ 个中选 $m$ 个，或者选 $m-1$ 个后再选第 $n$ 个。
$\sum\limits_{k=0}^m\dbinom{n+k}{k}=\dbinom{n+m+1}{m}$

实际上就是上一个递推式不断展开的结果。
$\sum\limits_{k=0}^n \dbinom km=\dbinom {n+1}{m+1}$

“上指标求和 (Summation on the upper index)”。对含 $m+1$ 的式子不断用递推式的方式展开，最后发现含 $m+1$ 项为 $0$，即可得到这个式子。
$\sum\limits_{i=0}^k\dbinom ni\dbinom m{k-i}=\dbinom{n+m}k$ 范德蒙德卷积
特别的，$\sum\limits_{k=0}^n\dbinom nk^2=\dbinom {2n}n$
$\sum\limits_{k=0}^k\dbinom kn\dbinom {r-k}m=\dbinom{r+1}{n+m+1}$。
$\dbinom nr\dbinom rk=\dbinom nk\dbinom{n-k}{r-k}$

组合意义。

1.3.3 插板法

$n$ 个相同小球，装进 $m$ 个不同盒子。不能为空。求方案数。

这也等价于 $x_1+x_2+\cdots+x_m=n,x_i\ge1$ 的方程解个数。

实际上，就是让我们在 $n-1$ 个缝隙之间，插 $m-1$ 个板子的方案数。即为 $\dbinom{n-1}{m-1}$。

那可以为空呢？

也就是 $x_1+x_2+\cdots+x_m=n,x_i\ge0$ 的方程解个数。

左右加 $m$，即为 $(x_1+1)+(x_2+1)+\cdots+(x_m+1)=n+m,x_i+1\ge1$。

答案即为 $\dbinom {n+m-1}{m-1}$。

1.3.4 Lucas 定理

对于质数 $p$，有 $\dbinom nm\equiv \dbinom{n / p}{m / p}\dbinom{n\bmod p}{m\bmod p}\pmod p$。

实际上就是把 $n$ 与 $m$ 写成 $p$ 进制数后计算的结果。

可用生成函数构造多项式证明。下文再提。

1.3.5 exLucas 定理

其实和 Lucas 没啥关系。

$p$ 不是质数的情况。根据唯一分解定理，必然可以将 $p$ 分解成 $p=\prod q_i^{\alpha_i}$，其中 $q_i$ 为质数。

于是我们只需求出质数幂次的值，再用 CRT 合并即可。

后面不会了，会了回来补。

1.3.6 常见组合数预处理

$\mathcal O(nm)$ 预处理 $n$ 行 $m$ 列的组合数，通常用于模数不是质数的情况。

1.4 预处理方法

1.4.1 模数为质数

预处理阶乘以及阶乘逆元即可。这是线性的。

1
2
3
4
5
6
7
8
9


 void prework (int n) {
     fac[0] = 1;
     for (int i = 1; i <= n; i ++) fac[i] = fac[i - 1] * i % p; ifac[n] = qpow W(fac[n], p - 2);
     for (int i = n - 1; ~i; i --) ifac[i] = ifac[i + 1] * (i + 1) % p;
 }
 int comb (int n, int m) {
     if (n < 0 || m < 0 || n < m) return 0;
     return fac[n] * ifac[m] % p * ifac[n - m] % p;
 }

1.4.2 Lucas 定理求解很大的情况

1
2
3


 int lucas (ll n, ll m) {
     return lucas (n / p, m / p) * comb (n % p, m % p);
 }

1.4.3 模数非质数

利用 Pascal 公式 $\mathcal O(n^2)$ 预处理。

1
2
3
4
5
6


C[0][0] = 1;
for (int i = 1; i <= n; i ++) {
    C[i][0] = 1;
    for (int j = 1; j <= n; j ++)
        C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % p;
}

1.5 例题

P2606 [ZJOI2010] 排列计数

求满足 $p_i>p_{\lfloor \frac i2\rfloor}$ 的排列个数。

注意到这个结构是一棵二叉树。所求即为二叉树小根堆的数量，考虑 DP。

设 $f(i)$ 为以 $i$ 为子树，满足小根堆的答案，$siz(i)$ 表示以 $i$ 为根的子树大小。那么根据乘法原理，有转移：$f(i)=f(lson)\times f(rson)\times \dbinom{siz(i)-1}{siz(lson)}$。

由于是二叉树的结构，因此可以将 dfs 转为线性递推，降低常数。注意 $m$ 不一定小于 $n$，故用 Lucas 防止组合数为 $0$。

1
2
3
4
5


for (int i = n / 2; i <= n; i ++) f[i] = 1, siz[i] = 1;
for (int i = n / 2; i; i --) {
    siz[i] = 1 + siz[i << 1] + siz[i << 1 | 1];
    f[i] = f[i << 1] * 1ll * max (1, f[i << 1 | 1]) % m * lucas (siz[i] - 1, siz[i << 1]) % m; 
}

*P6026 餐馆

转化一下，实际上就是求 $[1,n]$ 中选 $k$ 个不交区间的概率。

设 $f(k,r)$ 表示第 $k$ 次选的是以 $r$ 为右端点的概率，那么 $f(k,r)=\sum\limits_jf(k-1,j)\times\dfrac {1}{n}\times\dfrac{r-j}{r}$

然后打表发现答案是 $\dfrac{\dbinom{n}{k}}{n^k}$。

*P2059 [JLOI2013] 卡牌游戏

设 $f(i,j)$ 为 $i$ 个人坐成一圈，$1$ 为庄家，数 $j$ 个人的胜率。

考虑 $f(i-1)$ 与 $f(i)$ 的关系。

假设现在求 $f(i,j)$：枚举当前庄家抽到的牌 $k$，进而得到这一轮淘汰者的位置 $a$。

淘汰 $a$ 后，相当于在 $i-1$ 人组成的环中，原先的第 $j$ 个人在这个环中的获胜概率，也就是 $a+1$ 坐庄后，$j$ 的相对位置。考虑对 $a$ 与 $j$ 分类讨论。

若 $a<j$，那么 $a+1$ 坐庄，$j$ 就是其顺时针数 $j-a$，那么 $f(i,j)\gets f(i,j)+\dfrac {f(i-1,j-a)}m$。

若 $a>j$，那么就是 $a+1$ 到 $1$，$1$ 再到 $j$ 的位置。也就是 $i-a+j$。即 $f(i,j)\gets f(i,j)+\dfrac{f(i-1,i-a+j)}m$。

若 $a=j$，那么 $j$ 在这一轮被杀死，无贡献。

设 $f(i,j)$ 为 $[i-m+1,i]$ 状态为 $j$ 的方案数，我们令 $1$ 代表 C，并把新状态放在最高位上。那么有求和转移：$f(i,j)=\begin{cases}f(i-1,S_1),& S_1\text{ is vaild}\f(i-1,S_2),&S_2\text{ is vaild}\end{cases}$。其中，$S_1$ 与 $S_2$ 分别代表上一个合法状态。对于环形结构，相当于算 $n$ 次后状态不变。

由于 $n\le10^{15}$，考虑矩阵加速。构造 $2^m\times 2^m$ 的转移矩阵 $A$，每一行所对应的 $S_1$，$S_2$ 为 $1$。那么答案就是 $\sum A^n_{i,i}$。这题不应该紫啊，绿/蓝差不多。

P3862 数圈

考虑没有删边的 $n$ 点完全图圈数。

长度为 $i$ 的环等价于置换个数的一半（这个环时无向的），即 $\sum\limits_{i=3}^n \dbinom ni\dfrac{(i-1)!}2=\sum\limits_{i=3}^n\dfrac{n^{\underline i}}{2i}$，上方是下降幂。

由于是无向完全图，因此删除任何一边减去的贡献相同，不妨删掉边 $(u,v)$。考虑删边带来的影响。

考虑枚举这条边对每个长度圈的影响。实际上就是去掉 $u,v$ 两点的图中选 $i-2$ 个点，任意排列（因为加上 $u,v$ 后必然是新的置换）数，即 $\sum\limits_{i=3}^n \dbinom{n-2}{i-2}(i-2)!=\sum\limits_{i=3}^n\dfrac{(n-2)!}{(n-i)!}=\sum\limits_{i=3}^n(n-2)^{\underline {i-2}}$。

那么答案即为 $\sum\limits_{i=3}^n(n-2)^{\underline{i-2}}(\dfrac{n(n-1)}{2i}-1)$。当 $n\ge 9.99\times 10^8$ 时，下降幂到 $998244353$ 项就为 $0$。实际上 $i$ 只要计算到 $n-998244353+1$ 项，最大也只有不到 $1.8\times10^6$。

CF1946E Girl Permutation

单独把前后缀最大值提出来，发现是一个先递增，达到最值 $n$ 后递减的山峰状。

显然的，$a(p_{m_1})=a(s_1)=n$，我们就可以将整个排列独立地分成左右两部分，并给左右两边分配数值，也就是 $\dbinom{n-1}{p_{m_1}-1}$ 种方案。作为独立的一部分，自然可以看作一个新排列的答案。接下来讨论左边的情况。

独立地看左边，显然这是一个简化后的原问题：只不过最大值右侧可以随意填。设前缀最大值 $[1,i]$ 的答案为 $f(i)$，那么 $f(p_{m_i})=f(p_{m_{i-1}})\times\dbinom{p_{m_{i+1}}-2}{p_{m_{i+1}}-p_{m_i}-1}\times(p_{m_{i+1}}-p_{m_{i}}-1)!)$。特别的，$f(1)=1$。

对于右边也是类似的，也可以将序列与索引反转做一遍上述过程，假设后缀最大值 $[i,n]$ 的答案为 $g(i)$。则答案为 $f(p_{m_1})g(s_1)\dbinom{n-1}{p_{m_1}-1}$。

处理排列问题的通常思路，也就是将其划分成多个独立排列，划分成简单的子问题。

2. 容斥原理

容斥原理是十分强大的工具。可以将许多难以解决的计数问题变得简单明了。

2.1 基本形式

$$\lvert\bigcup\limits_{i=1}^n S_i\rvert=\sum\limits_{T\subseteq[1,n]\cap \mathbb N}(-1)^{\lvert T\rvert-1}\lvert\bigcap\limits_{t\in T}S_t\rvert$$

上式也就是：

$$f_S=\sum\limits_{T\subseteq S}g_T\iff g_S=\sum\limits_{T\subseteq S}(-1)^{\lvert S \rvert-\lvert T\rvert}f_T$$

$$f_S=\sum\limits_{S\subseteq T\subseteq U}g_T\iff g_S=\sum\limits_{S\subseteq T\subseteq U}(-1)^{\lvert T\rvert-\lvert S\rvert} f_T$$

2.2 容斥系数

尝试更广义地理解容斥。

我们希望求，在所有物品中，条件 $C_0$ 下的各物品贡献之和。

我们尝试构造容易计算贡献的条件 $C_1,\cdots,C_n$，再构造每个条件的容斥系数 $f_i$，使得对于所有物品有：$val(C_0)=\sum\limits_{i=1}^n val(C_i)f(i)$。其中 $val(C_i)$ 为条件 $C_i$ 下物品产生条件的贡献。

错排：求长度为 $n$ 使得任意 $p_i\not=i$ 的排列个数。

同样的，我们设 $C_i$ 表示至少有 $i$ 个位置不满足条件，也就是至少 $i$ 个位置满足 $p_i=i$。

2.3 “钦定”与“恰好”

假设我们有一个集合 $S={a_1,a_2,\cdots,a_n}$：

“恰好”有 $k$ 个元素。这部分对应的总方案是 $\dbinom nk$，也就是每一种 $k$ 个元素组成的子集个数。
“钦定”有 $k$ 个元素。我们先从钦定有 $a_i$ 入手。实际上，我们“钦定”了有元素 $a_i$，这一句话代表的集合是，所有包含 $a_i$ 的子集。进一步的，我们说"钦定"了 $k$ 个元素，实际上，是对于"恰好" $k$ 个元素的 $\dbinom nk$ 种集合的所有超集的可重和的结果。也就是说，钦定 $k$ 个元素所形成的集合，是一个可重集。

2.4 “钦定”与“恰好”的相互转换

我们已经说明”钦定“与”恰好“的定义。设 $f(i)$ 表示钦定有 $i$ 个元素，$g(i)$ 为恰好有 $i$ 个元素的。那么根据定义，有：

$$f(i)=\sum\limits_{j=i}^n\dbinom jig(i)\iff g(i)=\sum\limits_{j=i}^n(-1)^{j-i}\dbinom jif(i)$$

这就是经典的”二项式反演“。

如果我们继续定义“钦定”，“钦定至多”也类似的定义。我们设 $f(i)$ 表示钦定至多有 $i$ 个元素，$g(i)$ 仍为恰有 $i$ 个元素。那么有：

$$f(i)=\sum\limits_{j=1}^i\dbinom ijg(j)\iff g(i)=\sum\limits_{j=1}^i(-1)^{i-j}\dbinom ij f(j)$$

2.4.1 小应用：DAG 计数

easy version：求 $n$ 个点的 DAG 个数，$n\le 3000$。

考虑一个性质：一个 DAG 删掉入度为 $0$ 的点后仍为 DAG，于是将 DAG 分层。

设 $f_{n,i}$ 表示恰有 $i$ 个入度为 $0$ 的点的 $n$ 点 DAG 个数，$g_{n,i}$ 表示钦定有 $i$ 个入度为 $0$ 点的 $n$ 点 DAG 个数，$h_{i}$ 为 $i$ 个点的 DAG 个数。根据二项式反演，有：

$$g_{n,i}=\sum\limits_{j\ge i}\dbinom{j}{i}f_{n,j}\iff f_{n,i}=\sum\limits_{j\ge i}(-1)^{j-i}\dbinom{j}{i}g_{n,j}$$

而 $g_{n,i}=\dbinom ni 2^{i(n-i)}h_{n-i}$，含义是在 $n$ 个点选 $i$ 个入度为 $0$ 点，再在剩下的 $n-i$ 个点中决定连边情况。

$\begin{aligned}h_i&=\sum\limits_{j=1}^i f(i,j)\&=\sum\limits_{j=1}^i\sum\limits_{k\ge j}(-1)^{k-j}\dbinom kj g_{i,k}\&=\sum\limits_{j=1}^i\sum\limits_{k\ge j}(-1)^{k-j}\dbinom kj \dbinom{i}{k}2^{k(i-k)}h_{i-k}\&=\sum\limits_{k=1}^i\dbinom ikh_{i-k}2^{k(i-k)}[(1-1)^{k}-\dbinom k0(-1)^{k}]\&=\sum\limits_{k=1}^i(-1)^{k+1}\dbinom ikh_{i-k}2^{k(i-k)}\end{aligned}$

这是一个 $\mathcal O(n^2)$ 的做法。

medium version：求 $n$ 个点的弱连通 DAG 个数，$n\le3000$。

设 $h_{i}$ 为 $i$ 个点的 DAG 个数（不要求弱连通），$p_i$ 为 $i$ 个点的弱连通 DAG 个数。

其实做一步容斥就完了。

$p_i=h_i-\sum\limits_{j=1}^{i-1}\dbinom{i-1}{j-1}p_jh_{i-j}$，这里的 $j$ 是枚举包含点 $1$ 的分量大小。

hard version：求 $1\sim n$ 个点的弱连通 DAG 个数，$n\le 10^5$。

考虑一个 Trick：$ij=\dbinom {i+j}2-\dbinom {i}2-\dbinom {j}2$，组合意义显然。

那么 $2^{k(i-k)}=\dfrac{2^{\binom {i}2}}{2^{\binom k2}2^{\binom {i-k}2}}$。

可以 EGF！

于是 $\dfrac{h_i}{i!2^{\binom {i}2}}=\sum\limits_{k=1}^i\dfrac{(-1)^{k+1}}{2^{k\choose2}k!}\dfrac{h_{i-k}}{(i-k)!2^{i-k\choose2}}$

令 $\hat H(x)=\sum\limits_{i\ge0}\dfrac{h_i}{i!2^{i\choose 2}}x^i$，$\hat G(x)=\sum\limits_{i>0}\dfrac{(-1)^{i+1}}{i!2^{i\choose2}}$。

根据递推式，就有 $\hat F(x)=\hat F(x)\hat G(x)+1$，这里 $+1$ 是由于上式卷积没有 $k=0$。

进而解得 $\hat F(x)=\dfrac{1}{1-\hat G(x)}$。

接下来求

移项，有 $h_i=\sum\limits_{j=1}^i\dbinom{i-1}{j-1}p_jh_{i-j}$

那么有 $\hat P(x)=\ln\hat H(x)=\ln\dfrac{1}{1-\hat G(x)}$。

2.5 经典容斥

3. 生成函数

3.0 前置知识

3.0.1 广义二项式定理

若 $\alpha$ 是实数，对于所有 $0<|x|<|y|$，有

实际上，生成函数是无限可微分函数的 Taylor 级数。

3.0 前置知识

3.0.1 广义二项式定理

设 $\alpha$ 是实数，对于所有 $0\le|x|<|y|$，有

$$(x+y)^\alpha=\sum\limits_{k=0}^\infty \dbinom \alpha kx^ky^{\alpha-k}$$

其中

$$\dbinom{\alpha}{k}=\dfrac{\alpha(\alpha-1)\cdots(\alpha-k+1)}{k!}$$

设 $z=x/y$，那么定理可以等价地写作：对于满足 $|z|<1$ 的任意 $z$，有$$(1+z)^\alpha=\sum\limits_{k=0}^\infty\dbinom akz^k$$

假设 $n$ 为正整数，令 $\alpha=-n$，那么 $\dbinom{-n}{k}=\dfrac{-n(-n-1)\cdots(-n-k+1)}{k!}=(-1)^k\dfrac{n(n+1)\cdots(n+k-1)}{k!}=(-1)^k\dbinom{n+k-1}{k}$

因此，对于 $|z|<1$，有 $(1+z)^{-n}=\dfrac1{(1+z)^n}=\sum\limits_{k=0}^\infty(-1)^k\dbinom{n+k-1}kz^k$。

用 $-z$ 代替 $z$，有 $(1-z)^{-n}=\dfrac1{(1-z)^n}=\sum\limits_{k=0}^\infty\dbinom{n+k-1}kz^k$。

令 $n=1$，那么有 $\dfrac1{1-z}=\sum\limits_{k=0}^\infty z^k$。

3.0.2 多项式基础

$[x^n]F(x)$ 为 $F(x)$ 的第 $n$ 项系数。

几个运算：

$x^n =[x^n]F(x)+[x^n]G(x)$
卷积：$[x^n]F(x)G(x)=\sum\limits_{i=0}^n[x^i]F(x)\cdot[x^{n-i}]G(x)$

3.0.3 泰勒展开

3.1 普通生成函数 (Ordinary Generating Functions, OGF)

处理“无标号”计数。

3.1.1 定义

对于无穷数列：$a_0,a_1,\cdots,a_n,\cdots$

定义其生成函数为无穷级数：$F(x)=\sum\limits_{i=0}^\infty a_ix^i$，这是一个幂级数。

其封闭形式，指将无穷项转化为一个简洁代数式。如 $F(x)=\sum\limits_{i=0}^\infty x^i$，显然有 $xF(x)+1=F(x)$，进而解的其封闭形式为 $F(x)=\dfrac1{1-x}$。我们对于生成函数中的 $x$，以及 $F(x)$，我们不需要考虑 $x$ 的值与 $F(x)$ 值的联系。

3.1.2 常见 OGF 的封闭形式

常数序列 $a_i=1$，其 OGF 封闭形式为 $F(x)=\dfrac1{1-x}$。
几何级数：$a_i=A^i$，其 OGF 封闭形式为 $F(x)=\dfrac{1}{1-ax}$。
$F(x)=\sum\limits_{i=0}^\infty c^ix^{ik}$，其封闭形式为 $F(x)=\dfrac1{1-cx^k}$。
二项系数：$$\sum\limits_{n\ge k}{\dbinom nk}x^n=\dfrac{x^k}{(1-x)^{k+1}}$$。
Fibonacci 数列：$a_0=0,a_1=1,a_i=a_{i-1}+a_{i-2}$。其封闭形式为 $\dfrac {x}{1-x-x^2}$。

根据递推式，有 $x^2F(x)+xF(x)=F(x)-x$，即得 $F(x)=\dfrac x{1-x-x^2}$。

那怎么通过这个求 $a_i$ 的通项呢？

我们只需考虑如何从 $F(x)$ 的封闭形式推导出我们熟悉 OGF 的封闭形式即可。

注意到 $\dfrac{x}{1-x-x^2}$ 必然可以分解成 $\dfrac{a}{x-x_1}+\dfrac{b}{x-x_2}$ 这种形式，我们只需解出 $a,b,x_1,x_2$ 即可。也就是 $\begin{cases}a+b=1\ax_2+bx_1=0\x^2+x=1\end{cases}$，其中 $x_1,x_2$ 是第三个方程的一组根。解之，得 $\begin{cases}x_1=\frac{\sqrt5-1}2\x_2=\frac{-\sqrt5-1}2\a=\frac{5-\sqrt5}{10}\b=\frac{5+\sqrt5}{10}\end{cases}$。那么 $[x^n]F(x)$ 即为 $c_1^n+c_2^n=-(\dfrac a{x_1^{n+1}}+\dfrac{b}{x_n^{n+1}})$。代入即可。

从封闭形式到展开，我们可以直接通过广义二项式定理。

3.1.3 *求解线性齐次递推关系

定理：设 $q$ 非零。那么 $h_n=q^n$ 是下面常系数线性齐次递推关系

$$h_n-a_1h_{n-1}-a_2h_{n-2}-\cdots-a_kh_{n-k}=0$$

的解，当且仅当 $q$ 为方程 $x^k-a_1x^{k-1}$

唉没啥用就没写。

3.1.4 例

经典题

有 $1,2,5$ 元纸币若干，求恰组成 $n$ 元的方案数。

Sol

对于 $1$ 元，其生成函数为 $G_1(x)=1+x^1+x^2+\cdots$。

对于 $2$ 元，其生成函数为 $G_2(x)=1+x^2+x^4+\cdots$。

对于 $5$ 元，其生成函数为 $G_3(x)=1+x^5+x^{10}+\cdots$。

那么方案数即为 $[x_n][G_1(x)G_2(x)G_3(x)]$

为什么这是对的？

对于 $n$ 元的第 $k$ 项（特别的，我们设第一个为 $0$ 项），相当于选了 $k$ 个 $n$ 元，其指数也就是 $kn$ 元。根据乘法原理，卷积后的 $[x^n]F(x)$ 即为选 $n$ 元的方案数。

BZOJ3028 食物

依次用生成函数表示每一种食物，卷积即可。最终用广义二项式展开。

3.2 指数生成函数 (Exponential Generating Functions, EGF)

处理“有标号”计数。

3.2.1 定义

对于无穷数列：$a_0,a_1,\cdots,a_n,\cdots$

定义其生成函数为无穷级数：$\hat f(x)=\sum\limits_{i=0}^\infty a_i\dfrac {x^i}{i!}$。注意，EGF $\hat f$ 通常是与 OGF $f$ 区分的重要方式。

这种生成函数用于计数数列中比较适合，因为具有二项式定理的形式。在计数时，通常会求类似此类式子：$h(n)=\sum\limits_{i=0}^n\dbinom{n}{i}f(i)g(n-i)\iff\dfrac{h(n)}{n!}=\sum\limits_{i=0}^n\dfrac{f(i)}{i!}\cdot\dfrac{g(n-i)}{(n-i)!}$。

几个常见运算：

卷积：$\sum\limits_{i\ge0}f_i\dfrac{x^i}{i!}\sum\limits_{j\ge0}g_i\dfrac{x^i}{i!}=\sum\limits_{i\ge0}\sum\limits_{j=0}^i(f_jg_{i-j})\dfrac{x^i}{i!}$

积分：$\int\sum\limits_{n\ge0}f_n\dfrac{x^n}{n!}=\sum\limits_{n\ge1}f_{n-1}\dfrac{x^n}{x!}+C$

求导：$\dfrac{\mathrm{d}}{\mathrm dx}\sum\limits_{n\ge1}f_{n-1}\dfrac{x^n}{n!}=\sum\limits_{n\ge0}f_n\dfrac{x^n}{n!}$

3.2.2 常见 EGF

$\sum\limits_{n=0}^\infty \dfrac {x^n}{n!}=e^x$
$\sum\limits_{n=0}^\infty c^n\dfrac {x^n}{n!}=e^{cx}$
$\sum\limits_{n=0}^\infty n^{\underline k}\dfrac {x^n}{n!}=x^ke^x$
$\sum\limits_{n=0}^\infty \dfrac {x^n}{n}=\ln\dfrac1{1-x}$

3.2.3 Bell 数

贝尔数 $b_n$ 指的是将一个包含 $n$ 个带标号元素的集合，划分成任意数量的非空子集的方案总数。

下面提供两种推导 $\hat B(x)$ 的方法。

「基本块」的生成函数

我们称全集的一个非空子集为一个「块」。对于每个块构造 EGF，显然是 $\hat A(x)=\sum\limits_{i\ge1}\dfrac{x^i}{i!}=e^x-1$。

「划分」的生成函数

我们现在有了许多「基本块」，需要将其组合。$m$ 个块组合成一个集合只有一个方法，那么其生成函数 $\hat C(x)=\sum\limits_{i\ge0}\dfrac{x^i}{i!}=e^x$。

「合并」

综上所述，Bell 数的生成函数就是 $\hat C(\hat A(x))$，这是一个复合函数的形式。代入即得 $\hat B(x)=e^{e^x-1}$。

递推法

尝试写出 Bell 数的递推式：$b_n=[n=0]+\sum\limits_{j=1}^n\dbinom{n-1}{j-1}b_{n-j}$。

右侧是 $\hat B(x)$ 右移一位与 $e^x$ 卷积（也就是 $f_i=1$）的形式，所以有：

$$\begin{aligned}\hat B(x)&=1+\int \hat B(x)e^x\mathrm dx\\dfrac{\mathrm d\hat B(x)}{\mathrm dx}&=\hat B(x)e^x\\dfrac{\mathrm d\hat B(x)}{\hat B(x)}&=e^x\mathrm dx\\ln\hat B(x)&=e^x\mathrm + C\end{aligned}$$

由于 $b_0=0$，因此 $\hat B(0)=1$。进而解得 $C=-1$。

所以 $\hat B(x)=\exp(e^x-1)$。

有关 Bell 数的应用，见 2.5.1

3.2. 例

放球

$n$ 个不同球，放进四个不同盒子，使得第一个盒子有奇数个球，第二个盒子有偶数个球的方案。

Sol

$\begin{aligned}F(x)&=(1+x+\dfrac{x^2}{2!}+\cdots)^2(1+\dfrac{x^2}{2!}+\dfrac{x^4}{4!}+\cdots)(x+\dfrac{x^3}{3!}+\dfrac{x^5}{5!}+\cdots)\&=e^{2x}\cdot\dfrac{e^x+e^{-x}}{2}\cdot\dfrac{e^x-e^{-x}}{2}\&=\dfrac 14(e^{4x}-1)=\sum\limits_{i=0}^\infty4^{n-1}\dfrac{x^n}{n!}\end{aligned}$

这里用了两次泰勒展开，答案就是 $4^{n-1}$。

4. 特殊的数

4.1 Stirling 数

4.1.1 第一类斯特林数 (Stirling numbers of the first kind)

不如第二类常用。

$\begin{bmatrix}n\m\end{bmatrix}$：$n$ 个不同元素构成 $m$ 个互不区分的非空圆排列的方案数。
考虑新元素放在已有圆排列或者新开圆排列, 故有递推式：$\begin{bmatrix}n\m\end{bmatrix}=(n-1)\begin{bmatrix}n-1\m\end{bmatrix}+\begin{bmatrix}n-1\m-1\end{bmatrix}$。

$$n!=\sum\limits_{i=1}^n\begin{bmatrix}n\i\end{bmatrix}$$

排列与轮换一一对应。

4.1.2 第二类斯特林数 (Stirling numbers of the second kind)

$\begin{Bmatrix}n\m\end{Bmatrix}$：$n$ 个不同元素划分成 $m$ 个互不区分的非空子集的方案数。
新元素要么新开一个集合, 要么放在前面的集合中, 故有递推式：$\begin{Bmatrix}n\m\end{Bmatrix}=m\begin{Bmatrix}n-1\m\end{Bmatrix}+\begin{Bmatrix}n-1\m-1\end{Bmatrix}$.
通项公式为 $\begin{Bmatrix}n\m\end{Bmatrix}=\sum\limits_{i=0}^m\dfrac{(-1)^{m-i}i^n}{i!(m-1)!}$，可以用二项式反演推。

4.1.3 斯特林数恒等式

$$m^n=\sum\limits^m_{i=0}\begin{Bmatrix}n\i\end{Bmatrix}m^{\underline i}$$

左式的组合意义是 $n$ 个不同的球放到 $m$ 个不同的盒子的方案数（每个球有 $m$ 个选择, $n$ 个球, 故为 $m^n$ 种方案）.
右式则是枚举多少个盒子内有球, 求出这有球的 $i$ 个盒子排列数, 与其第二类斯特林数相乘后求和即为所求。
二者组合意义相同, 故有等式。
常用于处理 $m^n$ 形式。

下降幂、普通幂、上升幂

$$x^{\bar{n}}=\sum\limits_k \begin{bmatrix}n\k\end{bmatrix}x^{k}$$

$$x^n=\sum\limits_k\begin{Bmatrix}n\k\end{Bmatrix}(-1)^{n-k}x^{\bar{k}}$$

$$x^n=\sum\limits_k \begin{Bmatrix}n\k\end{Bmatrix}x^{\underline k}$$

$$x^{\underline{n}}=\sum\limits_k\begin{bmatrix}n\k\end{bmatrix}(-1)^{n-k}x^{{k}}$$

4.1.4 例题

P4609 [FJOI2016] 建筑师

考虑最大值左右，也就是在左边选 $A-1$ 个数作为前缀最大值，右边选 $B-1$ 个数作为后缀最大值。这显然是对称的，因此我们不妨考虑左边的数。这相当于我们把一些数分成 $A-1$ 组，假设有一组是为 $k$ 个，作为前缀最大值必须放在左边，后面可以随便放，有 $(k-1)!$ 种。多组，也就是将 $n-1$ 个数划分成 $A+B-2$ 个圆排列，方案数为 $\begin{bmatrix}n-1\A+B-2\end{bmatrix}$。

为什么是圆排列？因为我们规定了首个元素必须是前/后缀最大值，因此当后（前）$k-1$ 个元素任意调换顺序，都会构造出一个新的圆排列。

另外，我们再在选出的 $A+B-2$ 个前/后缀数，作为前缀。那么也就是 $A+B-2\choose A-1$。两者乘积即为答案。

P6162 [Cnoi2020] 四角链

先令 $n\gets n-1$。

设 $f(i,j)$ 表示在第 $i$ 为放了第 $j$ 个数的方案数。那么 $f(i,j)=\sum\limits_k f(k,j-1)\times(i-(j-1))$。设 $s(i,j)=\sum\limits_{k=1}^i f(i,j)$，那么转移式即为 $f(i,j)=s(i-1,j-1)\times (i-j+1)$，我们所求的是 $s(n,k)$。

注意到可以直接转化为关于 $s$ 的转移式，$s(n,k)=s(n-1,k-1)\times(n-k+1)+s(n-1,k)$。

这就是第二类 Stirling 数的递推式。因此 $s(n,k)=\begin{Bmatrix}n+1\n+1-k\end{Bmatrix}$。根据通项式 $s(n,k)=\sum\limits_{i=0}^k\dfrac{(-1)^{i+k}i^n}{(k-i)!k!}$ 计算即可，时间复杂度 $\mathcal O(k\log n)$。这个 $\log n$ 是计算 $i^n$ 带来的。

4.2 Catalan 数

4.2.1 通项式

在网格图上, 从 $(0,0)$ 向上向右走到 $(n,m)$ 的方案数？显然有 $n+m$ 次操作, 考虑向右是第几次操作, 答案则为 $\dbinom{n+m}{n}$.
在网格图上, 从 $(0,0)$ 向上向右走到 $(n,m)$, 不可经过直线 $y=x+1$ 的方案数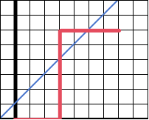？如图, 该为一个不合法的方案。我们在第一次交点后的图像沿 $y=x+1$ 翻折, 得到下图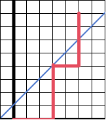：于是所有不合法的方案都是从 $(0,0)\to(n-1,m+1)$ 所有路径到达 $(n-1,m+1)$ 的路径上必然经过直线 $y=x+1$, 于是与不合法路径必然是一一对应的。故答案为 $\dbinom{n+m}{n}-\dbinom{n+m}{n-1}$.

特别的, 当 $n=m$ 时, 答案为 $\dbinom{2n}{n}-\dbinom{2n}{n-1}$, 这也就是 Catalan 数的第 $n$ 项, 记为 $C_n$。例题: [SCOI2010] 生成字符串
长度为 $2n$ 的合法括号序列数。我们将左括号视为向右走, 右括号视为向上走。于是转化为问题 2, 答案即为 $C_n$。
问题 2 加强, 不可经过两条直线 $y_1=x+b_1,y_2=x+b_2$ 的方案数？这玩意儿叫反射容斥，to be updated. 思路同理. 我们考虑容斥, $(0,0)\to(n,m)$ 的总方案数为 $\dbinom{n+m}{n}$. 那么最终答案呢？由于可能多次经过两条线, 我们分类为首先经过 $y_1$ 的方案 $ans_1$ 与首先经过 $y_2$ 的方案 $ans_2$. 最终答案即为 $\dbinom{n+m}{n}-ans_1-ans_2$. 我们只要计算出其中之一即可. 我们不妨计算以 $y_1$ 开头的答案. 仿照问题 2 的解决思路, 我们把终点沿着 $y_1$ 翻折得到 $(x’,y’)$, 减去 $\dbinom{x’+y’}{x’}$. 后沿 $y_2$ 翻折得到 $(x’’,y’’)$, 加去 $\dbinom{x’’+y’’}{x’’}$. 循环计算即可得到 $ans_1$, $ans_2$ 同理. 最终答案即为 $\dbinom{n+m}{n}-ans_1-ans_2$. 例题: [JLOI2015] 骗我呢将斜走法拉伸为水平, 后转化为此种类型.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


void rev (int& x, int& y, int b) { swap (x, y); x -= b; y += b; }
ll cacl (int b1, int b2, int n, int m) {
    int x = n, y = m, d = 1;
    ll res = choose (x + y, y);  
    while (x >= 0 && y >= 0) {
        if (d) rev (x, y, b1); else rev (x, y, b2);
        if (x < 0 || y < 0) break ;
        if (d) res = (res - choose (x + y, y) + p) % p;
        else   res = (res + choose (x + y, y) ) % p;
        d ^= 1;
    }
    x = n, y = m; d = 1;
    while (x >= 0 && y >= 0) {
        if (d) rev (x, y, b2);  else rev (x, y, b1);
        if (x < 0 || y < 0) break ;
        if (d) res = (res - choose (x + y, y) + p) % p;
        else   res = (res + choose (x + y, y) ) % p;
        d ^= 1;
    }   
    return res;
}

4.2.2 递归式

$n$ 个节点的二叉树, 有多少种形态？

设答案为 $f(n)$, 考虑左子树结点数与右子树结点数之和为 $n-1$, 故答案为 $\sum\limits_{i=0}^{n-1}f(i)f(n-1-i)$.

而 $f(n)=C_n$, 于是得到 Catalan 数的递归定义：$C_n=\sum\limits^{n-1}{i=0}C_iC{n-1-i}$.

4.2.3 几种定义式的互相转化

我们列出 Catalan 数的所有式子：

通项式：$C_n=\dbinom{2n}{n}-\dbinom{2n}{n-1}=\dfrac{1}{n+1}\dbinom{2n}{n}=\dfrac{1}{n+1}\sum\limits^{n}_{i=0}\dbinom{n}{i}^2$.
递归式：$C_n=\sum\limits^{n-1}{i=0}C_iC{n-1-i}$.
递推式：$C_n=\frac{4n-2}{n+1}C_{n-1}$.

其中 $C_0=C_1=1$.

证明

首先证明通项

$\begin{aligned}\dbinom{2n}{n}-\dbinom{2n}{n-1} & = \dbinom{2n}{n}-\dfrac{(2n)!}{(n-1)!(2n-n+1)!}\ & = \dbinom{2n}{n}-\dfrac{(2n)!n}{n!(2n-n)!(n+1)}\& =(1-\dfrac{n}{n+1})\dbinom{2n}{n}=\dfrac{1}{n+1}\dbinom{2n}{n}\end{aligned}$ 下证 $\dbinom{2n}{n}=\sum\limits^{n}{i=0}\dbinom{n}{i}^2$：设 $F(x)=(1+x)^n=\sum\limits^n{i=0}\dbinom{n}{i}x^i$, $G(x)=(1+\dfrac1x)^n=\sum\limits^n_{i=0}\dbinom{n}{i}(\dfrac1x)^i$.

$F(x)\cdot G(x)=[(1+x)\cdot(1+\dfrac1x)]^n=[\dfrac{x^2+2x+1}{x}]^n=\dfrac{(x+1)^{2n}}{x^n}=\dfrac{\sum\limits^{2n}_{i=0}\dbinom{2n}{i}x^i}{x^n}$.

则常数项为 $\dbinom{2n}{n}$.

将 $F(x)$ 与 $G(x)$ 的展开式直接相乘, 对应次数相乘之和即为常数项, 即为 $\sum\limits^n_{i=0}\dbinom{n}{i}^2$.

常数项相等, 即 $\dbinom{2n}{n}=\sum\limits^n_{i=0}\dbinom{n}{i}^2$.

递推式考虑展开即可得到通项式.

接下来证明递归式与通项式。

$\begin{aligned}F(x)&=\sum\limits_{i\ge0}C_ix^i\&=1+x\sum\limits_{i\ge1}\sum\limits_{j=0}^{i-1}C_jC_{i-1-j}x^jx^{i-j-1}\&=1+x\sum\limits_{i\ge0}\sum\limits_{j=0}^i C_jC_{i-j}x^jx^{i-j}\&=1+xF^2(x)\end{aligned}$

解得 $F(x)=\dfrac{1\pm\sqrt{1-4x}}{2x}$。

考虑 $\lim\limits_{x\to0}F(x)=1$，取正号显然不收敛。因此 $F(x)=\dfrac{1-\sqrt{1-4x}}{2x}$。

接下来用广义二项式展开。

$$\begin{aligned}F(x)&=\dfrac{1-(1-4x)^{1/2}}{2x}\&=\dfrac{1-\sum\limits_{i=0}^\infty\dbinom{\dfrac{1}{2}}{i}(4x)^i}{2x}\end{aligned}$$

$$\begin{aligned}\sum\limits_{i=0}^\infty\dbinom{\dfrac{1}{2}}{i}(4x)^i&=1+\sum\limits_{i=1}^\infty\dfrac{ (\dfrac12)^{\underline i} }{i!}(4x)^{i}\end{aligned}$$

哎呀我推不下去了以后补吧！

4.3 分拆数

实际上就是无标号方程解问题。

4.3.1 定义

分拆是将一个自然数写成若干有序正整数和的表示方式：$n=r_1+r_2+\cdots+r_k\ \ \ r_1\ge r_2\ge\cdots\ge r_k\ge1$。

$p(n)$ 表示自然数 $n$ 的分拆方法，如 $3=3,3=2+1,3=1+1+1$，共有三种分拆方式，即 $p(3)=3$。

特别的，$p(0)=1$。

$p(n,k)$ 表示自然数 $n$ 恰有 $k$ 部分分拆方法。

4.3.2 递推方法

$p(n,k)$ 的方案数同时是：$n-k=r_1+r_2+\cdots+r_k\ \ \ r_1\ge r_2\ge\cdots\ge r_k\ge0$ 的方案数。枚举有 $j$ 部分非零，恰有 $p(n-k,j)$ 个解，那么有和式：$p(n,k)=\sum\limits_{j=0}^k p(n-k,j)$，同理也有 $p(n-1,k-1)=\sum\limits_{j=0}^{k-1}p(n-k,j)$。二者作差得 $p(n,k)=p(n-k,k)+p(n-1,k-1)$，这个含义是比较显然的。要么在已有的 $k$ 个中都加 $1$，要么新增一个数。

4.3.3 生成函数

考虑每个数 $i$ 都能选任意多次，选 $i$ 的生成函数是：$\sum\limits_{n\ge 0}x^{in}=\dfrac1{1-x^i}$。

分拆的生成函数即为 $F(x)=\prod\limits_{i\ge 1}\dfrac{1}{1-x^i}$，$n$ 分拆的生成函数为 $F(x)=\prod\limits_{i=1}^n \dfrac{1}{1-x^i}$。

$k$ 部分 $n$ 分拆的生成函数是二元的，同样的，选 $i$ 的生成函数为 $\sum\limits_{j\ge0}y^jx^{ji}=\dfrac{1}{1-x^iy}$。

也就是 $F(x)=\prod\limits_{i=1}^\infty\dfrac1{1-yx^i}$，$p(n,k)=[x^ny^k]F(x,y)$。

4.3.4 例题

CF2125E Sets of Complementary Sums

5 Prüfer 序列

P5824 十二重计数法

$\textrm{I}$: 每个球选一个盒子，$m^n$。

$\textrm{II}$: $m$ 个盒子选 $n$ 个放球。$\dbinom mn n!$。

$\textrm{III}$: 考虑容斥。$f(i)$ 为钦定 $i$ 个为空的方案，显然有 $f(i)=(m-i)^nn!$。那么答案即为 $\sum\limits_{i=0}^m(-1)^{m+i}\dbinom{m}{i}(m-i)^nn!$

$\textrm{IV}$: 第二类斯特林数一行的和。

$\textrm{V}$: 假设答案为 ${{x_1},\cdots,{x_n}}$，显然只有一个集合。答案为 $[n\le m]$。

$\textrm{VI}$: 第二类斯特林数 $\begin{Bmatrix}n\m\end{Bmatrix}$。

$\textrm{VII}$: 插板法。$\dbinom{n+m-1}{m-1}$。

$\textrm{VIII}$: 实际上就是求哪些盒子装球。$\dbinom{m}{n}$。

$\textrm{IX}$: 插板法。$\dbinom{n-1}{m-1}$。

$\textrm{X}$: 就是分拆数。没解决。

$\textrm{XI}$: $[n\le m]$。

$\textrm{XII}$: 和 $\textrm{X}$ 一样。

Farthest City

在 $n\le500$ 个点的简单无向无权连通图上，设 $d_u$ 为 $1\to u$ 的最短路，求满足 $\forall i\in[1,n),d_i<d_n$ 的图的数量。

考虑分层，设 $f(i,j)$ 表示考虑了前 $i$ 个点，最后一层有 $j$ 个点的方案数，那么有转移： $f(i,j)=2^{j\choose 2}\sum\limits_{k=1}^{i-j}f(i-j,k)\times\dbinom{n-1-(i-j)}{j}\times(2^k-1)^j$

这个转移的含义依次考虑了：最后一层的 $j$ 个点之间有无边相连；在剩余非 $n$ 的点中选 $j$ 个；上一层的 $k$ 个点对这 $j$ 个点连多少条边，至少一条，因此减掉 $0$ 的情况。

1. 排列组合

1.1 基本计数原理

1.1.1 加法原理

1.1.2 乘法原理

1.2 排列数与组合数

1.2.1 排列数

1.2.2 组合数

1.2.3 多重组合数

1.3 组合技巧

1.3.1 二项式定理

1.3.2 组合恒等式

1.3.3 插板法

1.3.4 Lucas 定理

1.3.5 exLucas 定理

1.3.6 常见组合数预处理

1.4 预处理方法

1.4.1 模数为质数

1.4.2 Lucas 定理求解 很大的情况

1.4.3 模数非质数

1.5 例题

2. 容斥原理

2.1 基本形式

2.2 容斥系数

错排：求长度为 $n$ 使得任意 $p_i\not=i$ 的排列个数。

2.3 “钦定”与“恰好”

2.4 “钦定”与“恰好”的相互转换

2.4.1 小应用：DAG 计数

2.5 经典容斥

3. 生成函数

3.0 前置知识

3.0.1 广义二项式定理

3.0 前置知识

3.0.1 广义二项式定理

3.0.2 多项式基础

3.0.3 泰勒展开

3.1 普通生成函数 (Ordinary Generating Functions, OGF)

3.1.1 定义

3.1.2 常见 OGF 的封闭形式

3.1.3 *求解线性齐次递推关系

3.1.4 例

经典题

3.2 指数生成函数 (Exponential Generating Functions, EGF)

3.2.1 定义

3.2.2 常见 EGF

3.2.3 Bell 数

3.2. 例

放球

4. 特殊的数

4.1 Stirling 数

4.1.1 第一类斯特林数 (Stirling numbers of the first kind)

4.1.2 第二类斯特林数 (Stirling numbers of the second kind)

4.1.3 斯特林数恒等式

下降幂、普通幂、上升幂

4.1.4 例题

4.2 Catalan 数

4.2.1 通项式

4.2.2 递归式

4.2.3 几种定义式的互相转化

4.3 分拆数

4.3.1 定义

4.3.2 递推方法

4.3.3 生成函数

4.3.4 例题

5 Prüfer 序列

1.4.2 Lucas 定理求解很大的情况