我用了很久的头像。

Week 1

Sub 1

P10334

每个时刻可以制造任意体积果汁。

给出 $n$ 个人，每个人有来的时间 $t_i$ 和需求体积 $a_i$。需要使每个人来都有 $\ge a_i$ 的果汁，且每个人优先选最大体积果汁。来的顺序从左往右。最小化果汁体积和。

反过来考虑问题。不妨模拟每个人到达时的果汁。

这一过程可以从后向前做。维护栈 $s$，表示从后往前到 $i$ 累积的需求。由于每个人都取最大值，因此当前的人取得量应该是栈顶与自己的最大值。

每次当 $t_i>t_{i-1}$ 时，可以退栈，然后就做完了。

1
2
3
4
5
6
7

ll ans = 0;
for (int i = n; i >= 1; i --) {
    a[i] = max (a[i], a[ st[tp] ]);
    ans += a[i];
    st[++ tp] = i;
    while (tp && t[i] > t[i - 1]) -- tp, -- t[i];
}

P10875

给出无向图，多次询问 u v 至少需要前多少条边才会无割边。$n,q\le 3\times 10^5$。

此题多解啊！

不妨先把原图的时间最小的生成森林跑出来，然后强制不选生成树上的边。一个显而易见的性质是，每次选到边使树上有环，不必考虑森林的构成顺序，因为环上点必然在此之前连通（否则该边就成了树边）。

注意到这个东西，相当于使 $u\to v$ 路径上所有点合并，考虑用并查集维护这一过程：每次新增边就把链上点暴力合并，类似启发式合并的思想做这一过程。

对于查询，把所有询问挂在对应的两个点上，在暴力合并的过程中对合并点直接查询即可。具体来说，每次把路径上点合并到二者 LCA 上就可以。

P10680

给出 $n\le 2\times 10^5$ 个数 $p_i$。$Q\le 2\times10^5$ 次询问：

1. 1 i r 令 $p_i\gets r$。
2. 2 l k 取出 $l,l+1,\cdots,l+2^k-1$。每 $2i-1,2i$ 为一组，每组变为 $\vert p_{2i-1}-p_{i}\vert$。进行 $k$ 次，返回剩余的那个数。此操作不影响原序列。

不带修可以直接维护 ST 表。

带修怎么办？设 $2^{m}\le n<2^{m+1}$，对于 $k>\dfrac m2$ 与 $k\le\dfrac m2$ 的分别处理。

直接计算一段 $[l,l+2^k-1]$ 的复杂度，即 $\mathcal O(\sum\limits_{i=0}^{k-1} 2^i)=\mathcal O(2^k)$。考虑对 $k$ 分开处理：

• 若 $k\le\dfrac m2$，直接暴力计算，复杂度 $\mathcal O(\sqrt n)$。
• 若 $k>\dfrac m2$，维护所有块长为 $2^\frac{m}{2}$ 的值，那么计算的复杂度即为 $\mathcal O(2^{k-\frac m2})=\mathcal O(\sqrt n)$ 次。

每次修改，会影响到 $2^\frac{m}{2}$ 个值。我们同时维护长为 $2^1,\cdots,2^{\frac m2}$ 的值，长度为 $2^i$ 会有 $2^i$ 会被修改，即总修改次数为 $\sum\limits_{i=1}^\frac m2 2^i=2\sqrt n -1$。因此总复杂度为 $\mathcal O(q\sqrt n)$。

总结

从 14:37 开始写代码，到 15:04 才 AC。

主要以下错误：

修改函数写成 m«1，调了最久的 RE

st 表第一维写成下标了。。。

qry 函数把每一个位置都算了，导致一次查询复杂度干到 $\mathcal O(n\log n)$ 了。。

P13691

15:16 半个小时会 1 的做法，但是不会写代码。

15:43 发现找性质跳 $r_i$，但代码感觉很难写，然后就去看题解了。

17:56 贺了半天题解代码过了。

给出序列 $v_i,w_i$。对于 $i$，可以花费 $1$ 的代价使 $i$ 变成 $[i+1,i+v_i]$ 中任意一个数，或者花费 $2$ 的代价使 $i$ 变成 $[i+1,i+w_i]$ 的任意一个数。

$m$ 次询问，使 $A$ 变成 $B$，花费的最小代价。

$n,m\le 5\times 10^5$。

考虑没有第二种花费怎么做。

可以发现，如果当前跳不到 $B$，应优先跳 $r_i=i+v_i$ 最大的。设 $f(i,j)$ 表示从 $i$ 开始，跳了 $2^j$ 次可以跳到的最大点，易得转移式 $f(i,j)=\max\limits_{k=i}^{f(i,j-1)}f(k,j-1)$。显然，在查询时也需要用到这个东西，因此要保存下来（若在线）。考虑用 st 表，但这样空间与时间复杂度会到 $\mathcal O(n\log ^2n)$，那就用线段树存，显然是可以存的下的，但是常数较大，下面证明一个引理避免过大的内存开销。

引理 $f(i,j)=f(\arg\max\limits_{k=i}^{f(i,j-1)} r_k,j-1)$，$\arg\max$ 表示取到最大值时的下标。

证明：对于单次操作不能到达 $B$，跳 $k=\arg\max r_i$ 一定最优。这是因为对于 $i$，由于 $k\in(1,r_i]$，故当前步是可选 $[1,k)\cup{k}\cup (k,r_i]$ 的所有数。因而对于两个数的优劣，只需比较 $(r_i,r_k]$ 部分即可。显然 $r_k$ 越大越优。

故对于单次操作，跳 $r_i$ 尽量大的一定更优，因此每一步都选择跳 $\arg\max r_i$，因而每一步都这么跳可以使总结果最优。

而实际上每一次合并 $2^{j-1}\to2^j$ 都是将已经进行了 $2^j$ 次的两操作进行拼接，为保证步步最优，这一步一定要跳 $\arg\max r_k$。因此这就是对的。

证明这个引理过后，时空的复杂度就降到 $\mathcal O(n\log n)$，十分好写。

接下来考虑存在第二种花费的情况。

不存在第二种花费的根本就是因为，选择 $k\in[i,i+v_i]$，不会增加新的开销。而对于 $k\in(v_i,w_i]$，会增加 $1$ 的花销（假设 $w_i>v_i$），即使 $2^j$ 变成 $2^j+1$，这可不行啊！

于是考虑继续维护 $g(i,j)$ 表示跳 $2^j-1$ 步可达最远点。那么就增加了 $g(i,j)$ 与自己，$g(i,j)$ 与 $f(i,j)$ 相互间的转移情况：

1. $2^j=2^{j-1}+2^{j-1}$，和不存在第二种花费相同，但这里要多算一步，即 $r_i’=w_i+i$ 的情况。
2. $2^j=(2^{j-1}-1)+(2^{j-1}-1)+2$，即先跳两次 $2^{j-1}-1$ 步，最后再跳一个 $w_i$。
3. $2^j-1=2^{j-1}+2^{j-1}-1$，即先跳 $f$，再跳 $g$。这反过来也是一种情况。

以上都可以延续上面的引理来写。

对于查询操作，维护一个 $u$ 和一个 $v$。分别表示当前跳到的最远点，以及跳了记录次数 $-1$ 次的点。$v$ 的作用保证了跳 $w$ 不混乱。剩下的记录操作是经典的，没有见过的话可以理解为倍增 LCA 往上跳的操作。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

for (int i = 0; i < n; i ++) v[i] = min (n, i + 1 + v[i]), w[i] = min (n, i + 1 + w[i]);
for (int i = n; i; i --) v[i] = v[i - 1], w[i] = w[i - 1]; 
st[0].build (v), st[1].build (w); // st[0], st[1] 分别是以 v, w 建的 st 表
for (int i = 1; i <= n; i ++) f[i][0] = v[i], g[i][0] = i;
for (int j = 1; j <= 19; j ++) 
    for (int i = 1; i <= n; i ++) {
        int tmp = w[st[1].ask (i, g[i][j - 1])];
        f[i][j] = max ({f[ st[0].ask (i, f[i][j - 1]) ][j - 1], f[ st[1].ask (i, f[i][j - 1]) ][j - 1], 
                        tmp, g[ st[0].ask (i, tmp) ][j - 1], g[st[1].ask (i, tmp)][j - 1]}); // Case1 / Case2，其中与 tmp 作比实际上是对 j=1 的特殊判断，下 query 同
        g[i][j] = max ({f[ st[0].ask (i, g[i][j - 1]) ][j - 1], f[ st[1].ask (i, g[i][j - 1]) ][j - 1], 
                        g[st[0].ask (i, f[i][j - 1])][j - 1], g[ st[1].ask (i, f[i][j - 1]) ][j - 1]});
    } 

auto query = [&](int& l, int& r) {
    if (l == r) return 0;
    l ++, r ++;
    int u = l, v = 0, ret = 0;
    for (int j = 19; ~j; j --) {
        int uu = max (f[st[0].ask (l, u)][j], f[st[1].ask (l, u)][j]);
        int vv = u;
        if (v) {
            int tmp = w[st[1].ask (l, v)];
            uu = max ({uu, tmp, g[st[0].ask (l, tmp)][j], g[st[1].ask (l, tmp)][j]});
            vv = max ({f[st[0].ask (l, v)][j], f[st[1].ask (l, v)][j], vv});
        }
        vv = max ({g[st[0].ask (l, u)][j], g[st[1].ask (l, u)][j], vv});
        if(uu < r) u = uu, v = vv, ret |= 1 << j;
    }
    return ret + 1;
};

Sub 2

ARC201C

给出 $n$ 个 AB 串。对于每个前缀，求满足包含所有 AB 串前缀的子集个数。

$\sum\vert S_i\vert\le 5\times 10^5$。

唉，怎么看了 tag 呢。

在 Trie 上考虑这个问题。每次插入一个串，就在其于 Trie 末尾上 $+1$，设每个点的值为 $v_i$，子树 $v_i$ 和为 $sz_i$，$f_i$ 表示覆盖了 $i$ 子树内所有点的方案数。显然，这只会影响到末尾到根 $\mathcal O(\vert S\vert)$ 个点的 $f_i$ 值。这显然是一个二叉树结构，因此有转移式：

$$f_i=f_{ls}\times f_{rs}+2^{sz_{ls}+sz_{rs}}\times v_i$$

分别表示为不选/选当前节点的方案。

答案就是 $f_{rt}$，每次转移是 $\mathcal O(\vert S_i\vert)$ 的，总复杂度就是 $\mathcal O(\sum\lvert S_i\rvert)$。

ARC201B

$n$ 个物品，第 $i$ 个重量为 $2^{x_i}$，价值为 $y_i$。

选择任意多个重量和不超过 $W$ 的物品，求价值之和最大值。

$n\le 2\times 10^5$。

和这道题 P3188 [HNOI2007] 梦幻岛宝珠 基本是同一道题，思想也差不多，甚至这道题还是弱化版本。

设 $f(i,j)$ 表示选了代价 $j\times 2^i$ 的物品最大价值。对于当前层，我们仅对 $x_k=i$ 的物品 $k$ 进行转移，这一步是显然的，为 $f(i,j)=\max\limits_{x_k=i} f(i,j-1)+y_k$。

但是这玩意儿高达 $\mathcal O(n^2)$，显然是不行的。

由于所有重量都是 $2^k$，相当于二进制中的一位。那么可以断言，若当前二进制末尾为 $1$，则必然选重量为 $2^0$ 的物品，贪心地选，选价值最大即可。那么剩下的所有物品，可以贪心的按照大小顺序合并到 $2^1$ 上，并反复这个过程。

显然步步最优，故而全局最优。

ARC203C

给出 $n\times m$ 的网格图，相邻格子间有墙，被打破才能通过。从 $(1,1)$ 到 $(n,m)$，破 $k$ 个墙，有多少个破墙方法。

$n,m\le 2\times 10^5$。

$k\le n+m$。

先考虑最简路径，也就是类似 Catalan 数的方案数，即 $\dbinom{n+m-2}{n-1}$ 种，总共用了 $n+m-2$ 次机会。

因此 $k$ 至少是 $n+m-2$ 才有解，那么情况就变少了，对 $k$ 进行分类讨论：

• $k<n+m-2$，无解。
• $k=n+m-2$，即 $\dbinom{n+m-2}{n-1}$。
• $k=n+m-1$，再随便选一个门打开，即 $\dbinom{n+m-2}{n-1}\cdot\dbinom{2(n-1)\cdot(m-1)}{1}$。
• $k=n+m$。注意到此时可以将路径长度增加 $2$。
  • 若路径长度仍为 $n+m-2$，那么任选其他两个即可，即 $\dbinom{n+m-2}{n-1}\cdot\dbinom{2(n-1)\cdot(m-1)}{2}$。然而这显然会算重，即折角部分。考虑去重，把 $\rightarrow\downarrow$ 以及 $\downarrow\rightarrow$ 看作是 $\searrow$ 这一操作。就相当于在原本的 $n+m-2$ 次操作中减掉两次，再把 $\searrow$ 插入其中，即 $\dbinom{n+m-4}{n-2}\cdot(n+m-3)$，再强制选这一角的两边。因而这种情况的答案为 $\dbinom{n+m-2}{n-1}\cdot\dbinom{2(n-1)\cdot(m-1)}{2}-\dbinom{n+m-4}{n-2}\cdot(n+m-3)$
  • 若路径长度为 $n+m-2$，考虑在纵向还是横向多走两格，有 $\dbinom{n+m-2}{n+1}\cdot(n-1)+\dbinom{n+m-2}{m+1}\cdot(m-1)$。

ARC202C

设 $f(i) = \dfrac{10^i-1}{9}$。给出 $n$ 个数 $a_i$，对于每个 $k\in[1,n]，$求 $\operatorname{lcm}(f(a_1),f(a_2),\cdots,f(a_k))$。

$n,a_i\le 2\times 10^5$

Lemma 1. $\gcd (f(i),f(j))=f(\gcd(i,j))$。

Proof.

$\gcd(f(i),f(j))=\gcd(f(i)-f(j),f(j))=\gcd( \dfrac{10^i-10^j}{9},f(j) )=\gcd(10^j\times f(i-j),f(j))=\gcd(f(i-j),f(j))$

因而上式成立。

Lemma 2. $\operatorname{lcm}(S)=\prod\limits_{\empty\subseteq T\subseteq S} \gcd(T)^{(-1)^{\vert T\vert -1}}$

Proof.

考虑集合 $S$ 内数的一个质因子 $p$，设 $\min/\max_p(T)$ 表示 $p$ 的最低/高幂，根据 min-max 反演，有： $$p^{\max(S)}=p^{\sum\limits_{T\subset S}(-1)^{\vert T\vert +1}\min(T)}=\prod\limits_{T\subset S}p^{\min (T)\cdot(-1)^{\vert T\vert +1}}$$

设 $P$ 为 $S$ 中所有质因子组成集合，有： $$\operatorname{lcm}(S)=\prod\limits_{p\in P}p^{\max(S)}=\prod\limits_{p\in P}\prod\limits_{T\subset S}p^{\min (T)\cdot(-1)^{\vert T\vert +1}}=\prod\limits_{T\subset S}(\prod\limits_{p\in P}p^{\min (T)})^{(-1)^{\vert T\vert -1}}=\prod\limits_{T\subset S}\gcd(T)^{(-1)^{\vert T\vert -1}}$$

设 $S_i={a_1,a_2,\cdots,a_i}$，于是这道题就变成求 $\mathop{\operatorname{lcm}}\limits_{k\in S_i}f(k)=\prod\limits_{T\subset S_i}f(\gcd(T))^{(-1)^{\vert T\vert +1}}$，发现这个还是很难求。

设 $f(a)=\prod\limits_{d\mid a}g(d)$。有：

$$\begin{aligned}\prod\limits_{T\subset S_i}\left(\prod\limits_{d\mid\gcd(T)}g(d)\right)^{(-1)^{\vert T\vert +1}}&=\prod\limits_d\left(g(d)^{\sum\limits_{T\subset S_i\and d\mid \gcd(T)}(-1)^{\vert T\vert +1}}\right)\end{aligned}$$

把指数拿出来。多少个子集的 $\gcd$ 为 $d$ 的倍数，那么每个元素必然为 $d$ 的倍数。转化为对每个 $d$ 的倍数的集合计数问题，假设有 $k$ 个，枚举集合大小，有：

$$\sum\limits_{i=1}^k\dbinom ki(-1)^{k-1}=-(-1+1)^k+1$$

当 $k=0$ 时，此式为 $0$，当且仅当不存在元素为 $d$ 的倍数。其余均为 $1$。

问题就转化为 $\prod\limits_{d\in P}g(d)$，$P$ 是所有元素的因子集合。每次新增元素 $a_i$，遍历其所有因子，若没有出现过就乘上贡献。

剩下的问题就是求 $g(d)$，由于 $f(a)=\prod\limits_{d\mid a}g(d)$。两遍取对数，有 $$\ln f(a)=\sum\limits_{d\mid a}\ln g(a/d)\iff \ln g(a)=\sum\limits_{d\mid a}\mu (d)\ln f(a/d)\iff g(a)=\prod\limits_{d\mid a}\exp(\ln f(a/d)\cdot\mu (d))=\prod\limits_{d\mid a}f(a/d)^{\mu(d)}$$

然后就能开开心心做完这道题了。

Sub 3

ARC197C

给出包含所有正整数的无限集 $S$。

每次 $Q$ 次操作 $(A,B)$，先删掉 $S$ 中 $A$ 的倍数，再查询第 $B$ 小的数字。

$Q\le 10^5,2\le A\le 10^9,B\le 10^5$。

先钦定一个值域 $V$，每次筛掉 $V$ 内的数字。

显然，每次选的质数越小，删的越多。考虑删前 $1\times 10^5$ 个质数，跑了一下，发现 $V$ 取 $3\times 10^6$ 时能剩 $116817$ 个数。所以每次删就直接筛没被筛掉的，并统计。

这个可以用树状数组统计，查询直接在树状数组上二分即可。但我没写，$2\log $ 做法仍然跑的飞快。

ARC198C

给出长度为 $n$ 的序列 $A,B$。

可以对 $A$ 进行如下操作至多 $31000$ 次，使 $A=B$： 选择 $1\le i<j\le n$，使 $A_i\gets A_j-1$ ，$A_j\gets A_i+1$。

$2\le n\le100,A_i,B_i\le 100$。

首先，这一操作不会改变序列元素之和。

对于 $n\ge3$，总能通过不超过 $2nV$ 次操作将 $\ge3$ 的与 $B$ 匹配。具体的操作就是从后往前确定 $a_i$。

考虑 $n=3$ 的情况。注意到依次进行 $(1,3),(2,3),(1,2),(2,3)$ 操作相当于 $a_1\gets a_1-1,a_3\gets a_3+1$，反之亦然。假设 $a_3$ 已经匹配，只需先 $(2,3)$，再对 $(1,3)$ 进行操作。最后 $(2,3)$ 即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

void change (int x, int y) {
    a[x] ++, a[y] --;
    swap (a[x], a[y]);
    ope.emplace_back (x, y);
} 

void movel (int& x, const int& p) {
    if (x != 1) change (x - 1, x), x --;
    else change (1, x = p);
}

void mover (int& x, const int& p) {
    if (x != p) change (x, x + 1), x ++;
    else change (1, p), x = 1;
}

if (s1 != s2) return puts ("No") && 0;
if (n == 2) {
    if (a[1] == b[1]) return puts ("Yes\n0") && 0;
    if (a[1] == b[2] - 1) return puts ("Yes\n1\n1 2") && 0; 
    puts ("No");
    return 0;
}
int p = n, j = n;
while (p > 2) {
    while (a[j] > b[p]) movel (j, p);
    while (a[j] < b[p]) mover (j, p);
    if (j != p) {
        while (a[j] > b[p] - 1) movel (j, p);
        change (j, p);
    }
    j = -- p;
}

if (a[1] != b[1]) {
    change (2, 3);
    while (a[1] > b[1]) change (1, 3), change (2, 3), change (1, 2), change (2, 3);
    while (a[1] < b[1]) change (2, 3), change (1, 2), change (2, 3), change (1, 3);
    change (2, 3);
}

ARC200C

每个人有区间 $[l_i,r_i]$，选择一个排列，$p_i=k$ 表示第 $i$ 人选择作为 $k$。

每个人在 $l_i$ 时刻或 $r_i$ 时刻进入或退出，会影响在 $[1,k-1]$ 的人。

求排列，使被影响次数最少。

$n\le 500$。

考虑 $i,j$ 的贡献。

若 $[l_i,r_i]\cap[l_j,r_j]=\emptyset$，没有贡献。

若 $[l_i,r_i]$ 与 $[l_j,r_j]$ 相交但不包含，贡献恒为 $1$。

若 $[l_i,r_i]$ 包含 $[l_j,r_j]$，贡献为 $0$ 或 $2$。优先选 $0$，即使 $p_j<p_i$ 即可。

因此对第三种情况连边 $j\to i$ 表示 $j$ 先于 $i$。然后就转化为在满足限制下，最小化拓扑序的逆排序问题了。 直接 CF825E 即可。

ARC199C

给出 $m$ 个 $n$ 阶排列 $P_i$，求满足以下条件的树的数量：

• 对于树上任意两条边 $(u,v),(x,y)$，在 $1\to n$ 逆时针组成的圆环上，连接 $(p_{i,u},p_{i,v})，(p_{i,x},p_{i,y})$ 两边，除端点外，对于任意一组排列，无交。

$n,m\le 500$。

不妨钦定 $1$ 为根，问题就转化为对有根树的计数问题。考虑每个限制是在圆环上边的限制，故 $p_{i,j}$ 之间的相对大小不变，排列的效果也不变。即 $(p_{i,1}+k\bmod n) +1,\cdots,(p_{i,n}+k\bmod n)+1$ 与 $P_i$ 是等价的。令 $k=n-p_{i,1}$，这样就使所有 $p_{i,1}=1$。这一种钦定保证了下面的操作均为合法。

实际上一棵树，就是在圆环上选 $n-1$ 条边使每个点都连通。这道题限制了不能使边相交，考虑在什么情况下才会相交。在圆环上有一个经典结论，把边 $(u,v)$ 看作开区间，边有交等价于区间存在非包含的交关系。

也就是说，对于一条边 $(u,v)$，假设 $u<v$，存在 $p\in (u,v)$，使得 $q\not\in[u,v]$，有边 $(p,q)$ 则必然有交。继续考虑 $u,v$ 与 $p,q$ 的父子关系。枚举每种关系，发现无论在何种情况下，四者之一的子树内必然有在圆环上不连续的点。因此，不合法一定有子树内不连续。而子树内节点在圆环上不连续，很容易推出不合法。因此这个条件是充分必要的。

所以，所有合法条件，任意子树内的节点的所有映射在圆环上必然连续。根据这个性质考虑计数。把根去掉，圆环就成了一个线性结构。枚举根 $rt$，设 $f_{l,r}$ 表示根为 $rt$，其中 $[l,r]$ 为其组成子树的排列方案数。但是只有这一个东西显然没办法计数，考虑再设一个 $g_{l,r}$ 表示 $[l,r]$ 中组成森林个数。于是有 $f_{l,r}=\sum\limits_{rt} g_{l,rt-1}g_{rt+1,r}$，$g_{l,r}=\sum\limits_{rt}f_{l,rt}g_{rt+1,r}$。

但是如果直接做普通的 $[l,r]$ 跟条件毫无关联，甚至会忽略掉一些连续但在原排列中不连续的情况。考虑求出 $P_1$ 的逆排列，映射到其他排列上，并对于每个子区间预处理出合法情况即可。

最终答案是 $g_{2,n}$，这是由于前面已经钦定 $1$ 为根了。

Sub 8

P13842 篱莘龙

给出 $n$ 个有 $a_i,b_i$ 属性的奶龙。

对于每个前缀，求最大子集，使得 $\min\limits_{i\in S} b_i\ge \max\limits_{j\in S\setminus{i}} a_j$。

$n\le 10^6$。$a_i,b_i$ 互不相同。

考虑对于 $a_i<b_i$ 的情况怎么做。

设每个奶龙为坐标系上 $(a_i,b_i)$ 的点，那么答案就是使得 $y\ge k$ 且 $x\le k$ 围成矩形中点数量最多，每次新增点 $(a_i,b_i)$ 相当于对于区间 $[a_i,b_i]$ 加 $1$，查询即全局最大值。把这类点称作一类点。

引入 $a_i>b_i$ 的情况。

两种情况被直线 $l:y=x$ 划分为上下两部分，$a_i<b_i$ 的奶龙在 $l$ 上侧，$a_i>b_i$ 的奶龙在 $l$ 下侧。假设引入此类点 $(p,q)$，那么可以被加入的其他点为如下黄色的矩形区域。把这类点称作二类点。

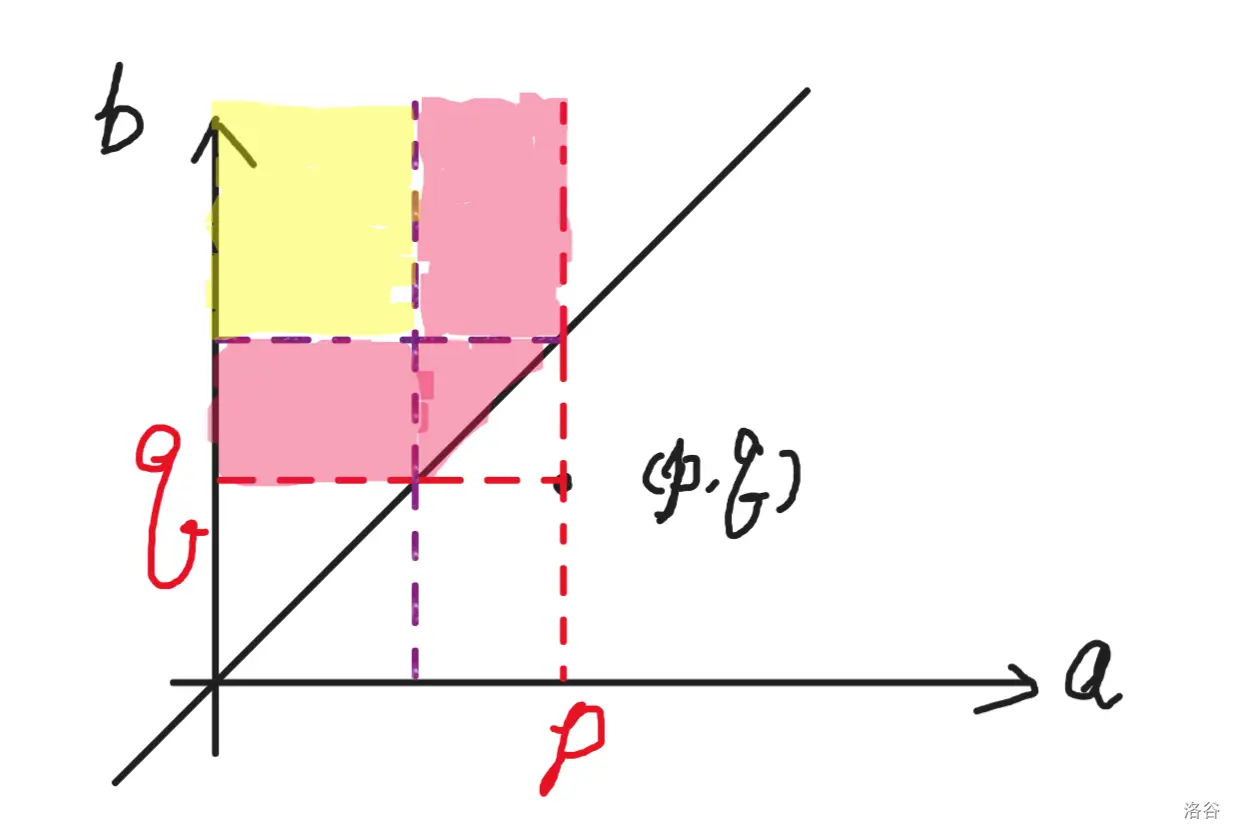
可以断言，当且仅当红色区域没有点时，取此类点才会更优，这是因为二类点的贡献至多是 $1$。也就是说，存在 $b_i\in(q,p)\and a_i\in[1,p)$ 或者 $a_i\in(q,p)\and b_i>q$ 的一类点时，就不统计这一贡献。

这个条件等价于任意二类点区间 $[q,p]$ 中不含一类点的端点，可以在两点处直接 $+1$。判断时直接用树状数组查询 $q,p$ 处前缀和是否相同即可。

另外，设两个二类点具有包含关系 $[p,q]\subset [u,v]$，那么显然，后者黄色区域更小，红色区域更大。故取更小的 $[p,q]$ 更优。这样维护的二类点一定没有包含关系的，故构成区间的 $r$ 与 $l$ 是正相关的。因此就可以用 set 维护区间。

对于每个区间，只需考虑是否取二类点。可以这样考虑，对于每个二类点 $[p,q]$，可以取的一类点满足 $q\in[a,b]$。由于前文已经排除 $a\in[p,q]$ 的情况，所以这就是对的。类比维护一类点最大贡献的方法，再开一个线段树来维护右端点为 $q$ 的二类点可取一类点的个数 $c$。答案为 $c+1$。

因此答案就是两棵线段树全局最大值的最大值。对于几个点要卡常，所以

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115

#include <set>
#include <ctime>
#include <vector>
#include <iostream>
#include <algorithm>

using namespace std;

int n;

struct SegmenTree {
    vector <int> t, lazy;

    #define ls (u << 1)
    #define rs (u << 1 | 1)
    #define mid (l + r >> 1)
    
    void init (int x, int k) { n = x; t.assign (n << 2 | 1, k); lazy.assign (n << 2 | 1, 0); }
    void upd (int u, int k) { t[u] += k; lazy[u] += k; }
    void pushdown (int u) { int& p = lazy[u]; if (p) upd (ls, p), upd (rs, p), p = 0; }
    void pushup (int u) { t[u] = max (t[ls], t[rs]);  }
    void add (int ql, int qr, int k, int u = 1, int l = 1, int r = n) {
        if (l >= ql && r <= qr) return upd (u, k);
        pushdown (u);
        if (ql <= mid) add (ql, qr, k, ls, l, mid);
        if (qr > mid)  add (ql, qr, k, rs, mid + 1, r);
        pushup (u);
    }
    int qry (int q, int u = 1, int l = 1, int r = n) {
        if (l == r) return t[u];
        pushdown (u);
        if (q <= mid) return qry (q, ls, l, mid);
        else          return qry (q, rs, mid + 1, r);
    } 
    void assign (int p, int k, int u = 1, int l = 1, int r = n) {
        if (l == r) return t[u] = k, lazy[u] = 0, void ();
        pushdown (u);
        if (p <= mid) assign (p, k, ls, l, mid);
        else          assign (p, k, rs, mid + 1, r);
        pushup (u);
    } 
} sgt, sgt2;

struct BIT {
    int n;
    vector <int> t;
    void init (int u) { n = u; t.assign (n + 1, 0); }
    void add (int u, int k) { for (; u <= n; u += u & -u) t[u] += k; }
    int qry (int u) { int ret = 0; for (; u; u -= u & -u) ret += t[u]; return ret; }
} bit;

set <int> p;
set < pair <int, int> > s2;

void insert (int l, int r) {
    if (bit.qry (r) - bit.qry (l - 1) > 0) return ;
    if (!s2.empty ()) {
        auto it = s2.lower_bound ({l, 0});
        if (it != s2.end () && it -> second < r) return ; // include others

        if (it != s2.begin ()) {
            auto itr = it;
            -- it;
            while (it != s2.begin () && it -> second > r) sgt2.assign (it -> second, 0), -- it; 
            if (it -> second < r) ++ it;
            else                  sgt2.assign (it -> second, 0);
            s2.erase (it, itr);
        }
    }
    sgt2.assign (r, 1 + sgt.qry (r));
    s2.insert ({l, r});
}

void clear (int l, int r) {
    if (!s2.empty ()) {
        auto it = s2.lower_bound ({l, 0}); 
        if (it != s2.begin ()) {
            auto itr = it;
            it --;
            while (it != s2.begin () && it -> second > l) sgt2.assign (it -> second, 0), -- it;
            if (it -> second < l) ++ it;
            else                  sgt2.assign (it -> second, 0);
            s2.erase (it, itr);
        }
        it = s2.lower_bound ({r, 0});
        if (it != s2.begin ()) {
            auto itr = it;
            it --;
            while (it != s2.begin () && it -> second > r) sgt2.assign (it -> second, 0), -- it;
            if (it -> second < r) ++ it;
            else                  sgt2.assign (it -> second, 0);
            s2.erase (it, itr);
        }
    }
    sgt2.add (l, r, 1);
    sgt.add (l, r, 1);
    bit.add (l, 1); bit.add (r, 1);
}

signed main (void) {

    auto st = clock ();

    int c, a, b; scanf ("%d%d", &c, &n); sgt.init (n << 1, 0); sgt2.init (n, 0); bit.init (n);
    for (int i = 1; i <= n; i += 2) {
        scanf ("%d%d", &a, &b);
        if (a > b) insert (b, a);
        else       clear (a, b);
        printf ("%d\n", max (sgt.t[1], sgt2.t[1]));
    }

    fprintf (stderr, "%.2fms.\n", (clock () - st) * 1000.0 / CLOCKS_PER_SEC);

    return 0;
}

Week 5

毫无目的的乱写。

P8252 [NOI Online 2022 提高组] 讨论

给出 $n$ 个集合 $S$，询问是否有集合有交但互不包含（不可相等），有输出一组即可。

$\sum\vert S\vert\le2\times10^6$。

考虑对每个集合排序，那么每个集合就可以映射到唯一的一条链上。

由于 $B\subseteq A\implies \vert B\vert\le \vert A\vert$，因此考虑从大到小建图。

注意到一个性质：若 $A,C$ 满足该性质，则 $A\subseteq B$，$B,C$ 也满足性质。

于是考虑枚举所有大小相邻且有交的集合，这样的复杂度不对。

​

USACO

24JAN G

Cowmpetency

有 $N$ 头牛，每个牛分配 $c_i\in[1,C]$ 的数。

给出 $Q$ 个关系 $(a,h)$，表示第 $h$ 头牛是首个比 $[1,a]$ 头牛严格大的牛。求方案数。

$N\le 10^9,C\le 10^4,Q\le 100$。

考虑这个关系的实际含义，即 $c_h>c_i,i\in[1,h)$ 且 $\max\limits_{i\in(a,h)},c_i\le \max \limits_{j\in[1,a]}c_j$。显然，$a$ 随 $h$ 呈单调增的关系。且任意 $(a,h)$ 对之间不含其他对。

于是按照对

23FEB G

Equal Sum Subarrays

宝宝题。

Fertilizing Pastures

对于 $T=0$，所有合法走的方式显然是任意一个欧拉序，时间为 $2(n-1)$。

对于 $T=1$，即遍历完所有点且可以不回溯回去，那么就是选一条最长链不回溯，时间为 $2(n-1)-l+1$，$l$ 为最长链长。

设 $f(u)$ 表示从时刻 $1$ 开始，走完 $\operatorname {subtree}(u)$ 的最小代价。设 $son_{u,p}$ 表示 $u$ 的第 $p$ 个子节点。实际上转移就是要确定一个最优排列 $P$，使得：

$$\sum\limits_{i=1}^{\vert son_u\vert}{f(son_{u,P_i})}+A(son_{u,P_i})\sum\limits_{j<i}2siz_{P_j}$$

其中 $A(u)$ 表示以 $u$ 为根的子树，$a_v$ 的和。$siz_i$ 表示子树 $i$ 的大小。

发现直接做是不好做的。考虑不等式的取值条件，假设 $\sigma$ 是最优序列，交换任意两项后必不优，化简后即

$$A(\sigma_{i+1})siz_{\sigma_i}\le A(\sigma_{i})siz_{\sigma_{i+1}}$$

发现可以直接按这个条件贪心。于是就做完了 $T=0$。

对于 $T=1$，$g(u)$ 也类似的设计。其中只有 $dep$ 取 $\max$ 的子树可以用 $g(u)$ 转移，其余均用 $f(u)$ 转移，且至多有一个 $g(u)$。用前缀和维护一下就好了。

Piling Papers

给出 $n$ 个数 $a_i$ 以及 $A,B$。多次询问，对于区间 $i\in[l,r]$ 的数 $a_i$，可以组成的在 $[A,B]$ 范围内的数的方案有多少。组成的数可以相同。

$n\le 300,1\le a_i\le9,A,B<10^{18}$。

朴素的想法是 $f_{i,k,0/1/2}$ 表示用前 $i$ 个数字填了 $k$ 位，小于/等于/大于上界的前 $k$ 位。但是发现没法往前面填。

于是考虑 $f_{i,l,r,0/1/2}$ 表示用前 $i$ 个数字填了 $[l,r]$ 位，且小于/等于/大于上界的方案数。注意到这就很容易写了。

对于每个 $i$ 都求出来这个值，每一轮是一个简单的 $\mathcal O(n\log^2 B)$ 的 dp。