2021 年的元旦和我的农历生日撞了，那天某个地方的照片。

介绍了简单图论的相关知识。

若连通：若一个有向图在边为无向时是连通图，那么这个有向图就是「弱连通」的。

拓扑排序

在一个 DAG（Directed Acyclic Graph，有向无环图）中，会呈现出递推关系。我们可以在这种图上进行一种遍历方式，即「拓扑排序（Topological Sorting）」。过程如下：

1. 将入度为 $0$ 的点加入队列；
2. 取队头，遍历所有出边，删除。直至队列为空。

每个点都有入队顺序，我们把这个顺序称作「拓扑序」。

例 P3573 [POI 2014] RAJ-Rally

设 $S_i$ 表示拓扑序在 $i$ 前的点的集合，$T_i$ 表示拓扑序在 $i$ 后的点的集合。枚举每个 $i$，那么最长路可能在 $S_i$、$T_i$ 或者是 $S_i\to T_i$ 中。

P3243 [HNOI2015] 菜肴制作

给出 DAG，求一种方案，使编号小的点拓扑序尽量小。

$n\le 10^5$。

一个显然的思路，是用小根堆来维护队列。然而很容易发现这个方法不对，这维护的是拓扑序的字典序尽量小，而题设是使其的逆置换尽量小，二者完全不同。

这个条件相当于每次找当前剩余的最小编号节点所在链，跑完这条链直到最小节点。如此循环往复下去，这样复杂度直接爆炸。考虑在反图上跑拓扑排序，那么这就相当于尽量晚地访问编号小的节点，即尽量早地访问编号大的节点。这就得到了这道题的做法。

AT_arc200_c [ARC200C] Movie Theater

每个人有区间 $[l_i,r_i]$，选择一个排列，$p_i=k$ 表示第 $i$ 人选择作为 $k$。

每个人在 $l_i$ 时刻或 $r_i$ 时刻进入或退出，会影响在 $[1,k-1]$ 的人。

求排列，使被影响次数最少。

$n\le 500$。

考虑 $i,j$ 的贡献。

若 $[l_i,r_i]\cap[l_j,r_j]=\emptyset$，没有贡献。

若 $[l_i,r_i]$ 与 $[l_j,r_j]$ 相交但不包含，贡献恒为 $1$。

若 $[l_i,r_i]$ 包含 $[l_j,r_j]$，贡献为 $0$ 或 $2$。优先选 $0$，即使 $p_j<p_i$ 即可。

因此对第三种情况连边 $j\to i$ 表示 $j$ 先于 $i$。然后就转化为在满足限制下，最小化拓扑序的逆排序问题了，即上一道题。

1. 最短路

1.1 几种最短路算法

1.1.1 Floyd 求多源最短路

要求：不存在负环。

设 $f(k,i,j)$ 表示经过 $1\sim k$ 节点，$u\to v$ 的最短路径长。

显然第一维可以滚掉。

1
2
3
4

for (int k = 1; k <= n; k ++)
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= n; j ++)
            f[i][j] = min (f[i][j], f[i][k] + f[k][j]);

小应用

最小环

• 枚举边 $(u,v)$，删除跑最短路，更新 $ans\gets \min(ans,dis_{u\to v}+w_{u\to v})$. $\mathcal O(n^2m)$ 或者 $\mathcal O(m(n+m)\log n)$
• Floyd 法。假设已经计算了经过 $1\sim k-1$ 的最短路，那么枚举所有小于 $k$ 的 $(i,j)$，令 $ans\gets\min (ans, dis_{i\to j}+w_{j\to k}+w_{k\to i})$。这样保证了三点不同，且 $(i,j)$ 的最短路径不含有 $k$。

传递闭包

1
2
3

for (int k = 1; k <= n; k ++)
    for (int i = 1; i <= n; i ++)
        if (f[i][k]) f[i] |= f[k];

这个可以用 bitset 优化。

1.1.2 Dijkstra 单源最短路

要求：不可解决含 负权 边的最短路。适用于单源最短路。

设 $dis_i$ 为源点到 $i$ 的最短距离。将点集划分成「已确定最短路」以及「未确定最短路」的集合，我们每次「已确定最短路」中 $dis_i$ 最小的 $i$，枚举其所有出边尝试更新别的点。当一个点被作为这种向外扩散时，这个点就被放入「已确定最短路」集合中。当「未确定最短路」集合为空，也就算完了。

如果直接枚举的话，复杂度为 $\mathcal O(n^2)$，这适用于稠密图。对于距离可以用优先队列优化，复杂度为 $\mathcal O(m\log m)$，适用于稀疏图。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

// 稠密图
void dijkstra (int s) {
    memset (dis, 0x3f, sizeof dis);
    dis[s] = 0;
    while (true) {
        int u = 0;
        for (int i = 1; i <= n; i ++) if (!vis[i] && dis[i] < dis[u]) u = i;
        if (!u) break ;
        vis[u] = true;
        for (auto [v, w] : g[u])
            if (dis[v] > dis[u] + w)
                dis[v] = dis[u] + w;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

// 稀疏图
void dijkstra (int u) {
    memset (dis, 0x3f, sizeof dis);
    priority_queue < pair <int, int> > q;
    q.push ({dis[u] = 0, u});
    while (!q.empty ()) {
        auto [d, u] = q.top (); q.pop ();
        if (vis[u]) continue;
        vis[u] = true;
        d = -d;
    	for (auto [v, w] : g[u])
            if (dis[v] > dis[u] + w) {
                dis[v] = dis[u] + w;
            	q.push ({-dis[v], v});
            }
    }
}

1.1.3 Bellman-Ford 单源最短路

要求：可以处理负环。

基本操作：「松弛」，即边更新操作：$dis_v=\min\limits_{u\to v\in E} (dis_v,dis_u+w_{u\to v})$ 可解决含负权边的问题，亦可判断有无负环。Ford 所做的，就是不断地对图里的每一条边尝试「松弛」。直到一轮中无法做松弛操作，那么就结束。每次扫一遍边是 $\mathcal O(m)$ 的，每次至少会使最短路边数增加 $1$，而最短路最多有 $n-1$ 条边，因此复杂度为 $\mathcal O(nm)$。

队列优化的 Bellman-Ford 最短路 —— SPFA

可以确定的一点是，每次能松弛的节点，一定是上一个被松弛的点。因此可以将这些点存在队列之中，尝试对其他点进行「松弛」。

特别的是，当一个点被松弛了 $n$ 次，那么一定是有负环，这就是一个判断负环的方法。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

bool spfa (int s) {
  	memset(dis, 0x3f, sizeof dis);
  	dis[s] = 0, vis[s] = 1;
  	q.push (s);
  	while ( !q.empty () ) {
    	int u = q.front();
    	q.pop (), vis[u] = 0;
    	for (auto [v, w] : e[u]) 
      		if (dis[v] > dis[u] + w) {
                dis[v] = dis[u] + w;
                cnt[v] = cnt[u] + 1; 
                if (cnt[v] >= n) return false;
                if (!vis[v]) q.push(v), vis[v] = 1;
      	}
  	}
  	return true;
}

1.1.4 Johnson 全源最短路

还没遇到，遇到细说。

可以处理负环负边权。就是先跑 SPFA 看有没有负环，然后再给每条边重新赋值，从每个点开始跑 Dijkstra。时间复杂度 $\mathcal O(nm\log m)$。

1.1.5 特殊边权最短路

边权为 $1$ 的最短路：直接 bfs。

边权为 $0/1$ 最短路：可以用双端 BFS 解决。对于边权较小的图，可以拆边/转化成 0/1 最短路。

1.2 最短路图与最短路树

在一个正权图中，从起点 $s$ 出发跑最短路，可以构造出一张 DAG，这个图叫做「最短路图」，可以进行拓扑排序等延伸操作。

到达 $v$ 的边有多条，不妨均只取一条，那么会构建出一棵树，即「最短路树」。

以下是例题。

1.2.1 例 P2149 [SDOI2009] Elaxia的路线

首先，最长公共路径一定是图上的一条链：假设不是一条链，而是分成两段，那么间隔两段的路径长度必然相同，否则不符合最短路的要求。而路径相同我们不妨就选择相同的一段路，这样仍为一条链。

因此，我们只需在两条最短路的任意一条最短路图上找与另一张图交的最长链即可。

用 Dijkstra 构建出最短路图，是一个 DAG，因此找最长交链可以用 DAG 上 DP 做，可以用 DFS 遍历所有在最短路图上的边。

然而，我们可能在 DP 过程中出现如下这种情况。

$s’\to t’$ 有两种不同路径，但是在拓扑 DP 时会错误地判断两条不同路径形成一条链。我们只需对于两个图都跑一遍 DP 后取结果最小值即可。

code

1.2.2 例 CF1076D Edge Deletion

构建最短路树，树上 DP。$f_i$ 表示边 $i$ 的儿子数。从小到大排序，前 $k$ 个即为答案。

code

1.2.3 例 P6880 [JOI 2020 Final] オリンピックバス

可先求出以 $1$ 为起点的 $dis_1$ 以及以 $n$ 为起点的 $dis_2$。我们再求出相应反图对应的 $dis_3$ 与 $dis_4$。至于为何需建立反图，详见下文。

用 Dijkstra 构建最短路树。则若要翻转的边在这个树上，对答案有影响；反之，无影响。而最短路树只有 $n-1$ 条边，故我们在当且仅当边 $E$ 在上面提到的四个最短路树上时，才需要重新 Dijkstra。总复杂度仅为 $\mathcal O(n^3)$。

于是答案便是显然的。设 $val(dis_k,ed,i)$ 代表翻转第 $i$ 边，第 $k$ 个最短路树从起点到 $ed$ 的最短距离。于是每次枚举翻转边。对于当前翻转边 $E:(u\to v,w)$，在 $1\to n$ 的路径上，我们可以选择不走这条翻转边，花费即为 $val(dis_1,n,E)$；我们亦可走这条边，即 $val(dis_1,v,E)+w+val(dis_4,u,E)$。此时反图的原因就显然了。由于在求解时需要求这个有向图任意点到 $n$ 的最短路，所以等价于反图中 $n$ 到任意点的最短距离。在 $val$ 函数中亦适用。$n\to1$ 的情况同理。故翻转答案为：

$$\min\limits_{E\in G}{\min[val(dis_1,n,E),val(dis_1,v,E)+w+val(dis_4,u,E))]+\min[val(dis_2,1,E),val(dis_2,v,E)+w+val(dis_3,u,E))]+D_E}$$

与不翻转边的答案求最小值即为所求。

code

1.2.4 例 ABC416E Development

将机场作为一个点 $N+1$，机场点就相当于与 $N+1$ 有一条 $\dfrac T2$ 的边。每次新建 $(u,v)=T$，枚举两点 $(x,y)$，$d_{x,y}\gets\min(d_{x,u}+T+d_{v,y},d_{x,v}+T+d_{u,y},d_{x,y})$。建机场就是 $(u,N+1)=\dfrac T2$。

判重边！！！

1.3 与最短路结合的 DP

1.3.1 例 P4745 [CERC2017] Gambling Guide

设 $f_i$ 表示从 $i$ 到 $n$ 的最小期望。若 $f_u>f_v$，那么 $f_v$ 会影响 $f_u$ 的值，$f_u$ 不会影响 $f_v$ 的值。因此我们需要从小往大转移。

考虑转移。我们枚举 $u$ 的每一条边，如果 $f_u>f_v$，则 $f_v$ 可以对 $u$ 产生贡献；反之，我们不如在原地等待。那么有 $f_u=\dfrac 1{deg_u}\sum\limits_{(u,v)\in E}\min(f_u,f_v)+1$。

用 Dijkstra 的方式，以 $f_u$ 为第一关键字维护队列即可。

code

1.4 次短路

对于正权图，有两种做法。

• 维护最短路的同时维护次短路。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

void Dijkstra (int st) {
    memset (dis, 0x3f, sizeof dis);
    priority_queue <Node> q;
    vis[st] = true; q.push ({st, dis[0][st] = 0});
    
    while (!q.empty () ) {
        auto d = q.top ().dis, u = q.top ().u; q.pop ();
        if (d > dis[1][u]) continue;
        for (auto e : g[u]) {
            int v = e.first, w = e.second;
            if (dis[0][v] > d + w) {
                dis[1][v] = dis[0][v];
                q.push ({v, dis[0][v] = d + w});
            } else if (dis[1][v] > d + w && d + w > dis[0][v]) 
                q.push ({v, dis[1][v] = d + w});
        }
    }
}

• 跑两遍最短路，枚举边 $(u,v)$，计算 $\min{w_{u\to v}+d_{s\to u}+d_{v\to e}}$，不得小于最短路。

1
2
3
4
5
6
7

dijkstra (1, 0); dijkstra (n, 1);
for (int i = 1; i <= n; i ++) 
	for (auto [v, w] : g[i]) {
		if (risky[i] || risky[v]) continue;
		ll val = w + d[0][i] + d[1][v];
		if (val > d[0][n]) ans = min (ans, val);
	}

例题：P2829 大逃离

1.5 同余最短路

https://www.luogu.com.cn/article/67f6rys1

例 P3403 跳楼机

给定 $x,y,z,h$，对于 $k\in[1,h]$，求满足 $\mathbb Z_+$ 上 $ax+by+cz=k$ 的 $k$ 个数。

不妨设 $x\le y\le z$，那么题意等价于：满足不定方程 $by+cz\equiv k\pmod x$ 的 $k\in[1,h]$ 的数量。我们求出最小 $d_i=by+cz$ 使得 $d_i\equiv i\pmod x$，那么所有 $k\in[1,h]$ 中模 $x$ 为 $i$ 的数量为 $\left\lfloor \dfrac{h-d_i}x\right\rfloor+1$。

求这个最小值 $d_i$，跑一遍最短路即可。即对于每个 $i$ 建一条 $i\overset{y}{\longrightarrow}(i+y)\bmod x$ 的边。

与这道题几乎一样的，可以看看 P2371 [国家集训队] 墨墨的等式 。

ABC077D Small Multiple

TBD。

1.6 差分约束

1.6.1 算法简介

差分约束是一种求解形如

$$\begin{cases}x_{a_1}-x_{b_1}\le c_1\\x_{a_2}-x_{b_2}\le c_2\\\dots\\x_{a_n}-x_{b_n}\le c_n\end{cases}$$

不等式一组解的算法。

注意到 $x_a-x_b\le c_1\iff x_a\le x_b+c$ 与单源最短路中的三角不等式 $d_a\le d_b+w_{b\to a}$ 十分类似。故考虑对每一组限制建一条 $b_i\overset{w=c_i}{\longrightarrow} a_i$ 的边，并建立超级源点 $S$，从 $S$ 向每个点连一条权值为 $0$ 的点。

从 $S$ 跑单源最短路，这样就能求出不等式的一组最小解。若存在负环，那么无解。

特别的，我们也可转化为 $x_a+(-c)\le x_b$，这相当于建 $b\overset{w=-c}{\longrightarrow}a$ 的边，跑最长路的一组最大解。如果有正环，那么同样的，无解。

2. 生成树

2.1 最小生成树

最小生成树有三种求法，你，知道么？

2.1.1 Kruscal

基于一种贪心思想，每次优先选边权最小的来连通两个联通块，直到将所有点都连通。用并查集维护连通快。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

struct edge { int u, v, w; };

int Kruscal (vector <edge> e) {
    sort (e.begin (), e.end (), [&](auto x, auto y) { return x.w < y.w; });
    int res = 0;
    for (auto [u, v, w] : e) {
        if (find (u) == find (v)) continue;
        merge (u, v);
        res += w;
    } 
    int cnt = 0;
    for (int i = 1; i <= n; i ++) if (fa[i] == i) ++ cnt;
    if (cnt != 1) return -1; // 不连通 
    return res;
}

Prim

Prim 的思想是，从一个点开始，不断加点。也就是维护一个连通块，每次找与这个连通块最近的的点，加入联通块。这和 Dijsktra 的过程十分相似。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

int prim (int u) {
    memset (dis, 0x3f, sizeof dis);
    priority_queue < pair <int, int> > q;
    q.push ({-dis[u], u}); int cnt = 1, res = 0;
    while (!q.empty ()) {
        if (cnt >= n) break ;
        auto [d, u] = q.top (); q.pop ();
        if (vis[u]) continue;
        vis[u] = true;
        ++ cnt;
        d = -d;
        res += d;
    	for (auto [v, w] : g[u])
            if (dis[v] > w) {
                dis[v] = w;
            	q.push ({-dis[v], v});
            }
    }
}

Boruvka

Boruvka 结合了 Kruscal 与 Prim 的思想，在具有特殊性质的完全图中，可搭配相应的数据结构使用。具体的思想，即维护已经选择的边组成的连通块集合，每次选择与连通块相连的边中权值最小的合并

具体来说，每一轮如下环节：遍历所有不在同一连通块的边 $(u,v)$，用这条边的边权更新 $u$ 与 $v$ 所在连通块与其他连通块相连的最小边。如果不存在，那么就说明已经结束。

由于每次连通块个数至少减半，因此复杂度为 $\mathcal O(m\log n)$。

图源 OI-Wiki。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

bool comp (int x, int y) {
    if (w[x] != w[y]) return w[x] < w[y];
    return x < y;
}

void Boruvka () {
    for (int i = 1; i <= n; i ++) fa[i] = i;
    bool upd = true;
    while (upd) {
        upd = false;
        memset (best, 0, sizeof best);        

        for (int i = 1; i <= m; i ++) {
            if (used[i]) continue;
            int p = find (u[i]), q = find (v[i]);
            if (p == q) continue;
            if (comp (i, best[p])) best[p] = i;
            if (comp (i, best[q])) best[q] = i;
        }

        for (int i = 1; i <= n; i ++) {
            if (best[i] && !used[ best[i] ]) {
                used[ best[i] ] = true;
                ++ cnt;
                upd = true;
                ans += w[ best[i] ];
                fa[ find (u[ best[i] ]) ] = find (v[ best[i] ]);
            }
        }
    }
}

2.1.2 例题

P2700 逐个击破

正难则反。对标记的点做最大生成树即可。

P3623 [APIO2008] 免费道路

注意要求的同时性。我们需要满足：最终结果是一棵树，恰有 $K$ 条鹅卵石路，图连通，任一不满足输出 $\texttt{no solution}$。

我们先把所有水泥路做一遍生成树。这样，若有解，图仍不连通，那么必然有鹅卵石路将几个连通块连通，这样我们就筛选出了所有必须的鹅卵石路。接下来去掉所有水泥路的边，加鹅卵石边直至 $K$。最后，我们再对水泥路跑生成树即可。

P5633 最小度限制生成树

大体思路：和上题一样，我们先求在无 $s$ 的图上跑 Kruscal，这样我们能求出所有可能保存的边。之后枚举所有连通块中的所有点，就能筛出所有必须的与 $s$ 相连的最小边。最后贪心地调整删边，在保持合理的情况下，就能解除答案。

我们分别考虑如下问题：

1. 如何维护连通块？ 令 $val_i$ 表示 $i\to s$ 的边权，不存在为 $+\infin$。让 $val$ 值更大的连向 $val$ 值更小的。那么所有连通块的顶即为与 $s$ 相连最小权的点。
2. 该删怎样的边？ $val_i-w_{i\to v}$ 代表用 $i\to s$ 代替 $i\to v$ 的代价，我们希望这个代价尽量小，这就是我们想要删的边。
3. 如何实现删边？ 对于树中边 $u\to v$，假设其连接了连通块 $x,y$。因为已经连通，所以我们删边更大的那一部分，因为根据贪心，我们必然是在更小的那个块与 $s$ 连通。因此，我们再连接两个连通块时，我们把 $u\to v$ 的边权放在更大的那个连通块上，我们设这个值为 $k$。那么代价即为 $val_i-k_i$。

最终，我们找到前 $k-P$ 小的 $val_i-k_i$，其中 $P$ 为将森林连成树的边数，加入答案即可。

P8207 [THUPC 2022 初赛] 最小公倍树

特别好玩的一道题啊。

$(u,v)$ 的边权为 $\operatorname{lcm}(u,v)=\dfrac {u\times v}{\gcd(u,v)}$，考虑枚举 $d=\gcd(u,v)$。对于每个 $d$，设 $k$ 是首个满足 $l\le kd\le r$，那么所有 $l\le(k+P)d\le r$ 的 $(k+P)d$ 连边，这些边是最终树的一个超集。假设存在 $\operatorname{lcm}[(k+k_0)d,(k+P_0)d]<\operatorname{lcm}[(k+k_0)d,(k+P_0)d]$，那么 $(k+k_0)d$ 与 $(k+P_0)d$ 存在更大的公约数。在后面枚举新的 $d$ 时，必然可以连边。我们就保证边的充分性。之后跑 Kruscal 即可。

总边数为 $\mathcal O((R-L)\ln R)$，约在 $2\times 10^6$ 这个量级，可以接受。 和这题很像的是 CF2081D MST in Modulo Graph ，做法都是一样的！但是注意要先枚举 $p$ 再计算相应 $k$ 的首个余数 $d$。

CF1550F Jumping Around

假设 $u$ 可以直接跳到 $v$，那么就是：

$$\begin{aligned} &d-k\le\vert a_u-a_v\vert\le d+k \\ &-k\le\vert a_u-a_v\vert-d\le k \\ &\lvert \vert a_u-a_v\vert -d\rvert \le k\end{aligned}$$

我们对每个石头抽象为图上一点，$(u,v)$ 边的边权设为 $\lvert \vert a_u-a_v\vert -d\rvert$，那么对于 i k 而言，实际上就是 $s\to i$ 的路径上是否边权均不超过 $k$。根据最小生成树的性质，这就是在最小生成树的简单路径上判断最大值。对于完全图，考虑使用 Boruvka。

在 Boruvka 找连通块与外界相连的最小边的过程中，我们注意边权的特殊性质。固定 $u$，对于 $a_v<a_u$，边权 $w=\vert a_u-a_v-d\vert=\vert a_u-d-a_v\vert$；对于 $a_v\ge a_u$，边权 $w=\vert a_v-a_u-d\vert=\vert a_u+d-a_v\vert$。也就是说，我们找距离 $a_u+d$ 或者 $a_u-d$ 最近的 $a_v$ 就能最小化边权。考虑二分。但是对于同一连通块内的元素不好处理，因此考虑使用 set 维护。

初始 set 中存所有点。枚举到一个连通块时，删掉 set 中连通块内的所有点。之后对于连通块内所有点二分查找最近的 $a_v$ 并更新。结束后放回 set 中。

一轮下来，时间复杂度为 $\mathcal O(n\log n)$。最多 $\log n$ 轮，故时间复杂度为 $\mathcal O(n\log^2n)$。

2.2 次小生成树

2.2.1 「非严格」次小生成树

假设初始最小生成树边权和为 $S$。枚举所有非树边 $(u,v,w)$，计算树上 $u\to v$ 路径上最大边权 $w’$，更新 $S’\gets \min(S’-w’+w)$。

对于最大边权，类似倍增 LCA 的方法维护每个点到 $2^i$ 级祖先的最大边权，这样在求 LCA 的同时也能求出最大边权。

2.2.2 「严格」次小生成树

P4180 [BJWC2010] 严格次小生成树

和「非严格」次小生成树类似，我们只需对于每条非树边 $(u,v,w)$ 求 $u\to v$ 简单路径上「严格」次大边权即可。

对于这一操作，可以仿照 1.4 次短路的写法来做。

2.3 Kruscal 重构树

2.3.1 定义

Kruscal 时，对于要连边的 $u,v$ 不直接连边，而是新增虚拟节点 $T$，点权为要连边的边权。将 $u$ 与 $v$ 所在集合的根节点设为 $T$ 的左右儿子。将 $T$ 定义为这个新集合的根。

在 $n-1$ 轮后，这就形成了一棵 二叉树。这棵二叉树就是 Kruscal 重构树。

2.3.2 性质

1. 有 $n$ 个叶子的二叉树。
2. 可以看作是 大根堆，将叶子权值视作正无穷。
3. $u\to v$ 路径最大值的最小值为 Kruscal 重构树上二者 LCA 的权值。
4. 对于 $u$，设 $v$ 是距离 $u$ 最远的满足 $w_v\le w$ 的 $u$ 的祖先，那么 所有 $u$ 经过权值 $\le w$ 的边能够达到的最远集合恰好为 $v$ 子树内的所有叶子结点。这个性质可以将某些连通性问题转化为子树问题，可以通过 dfs 序套数据结构维护。

2.3.3 例题

P4768 [NOI2018] 归程

首先，用 Dijsktra 预处理出 $1$ 到其他节点的最短路 $d_x$。按照海拔从大到小排序，构造 Kruscal 重构树。

根据性质 4，一次查询 v p 相当于找到 $v$ 的最浅的使得海拔高于 $p$ 的祖先 $u$。以 $u$ 为根的子树内的叶子结点，就是仅经过海拔 $>p$ 的边的所有点。我们对每个子树 $u$ 维护 $\min\limits_{x\in subtree(u)} d_x$ 即可。

当然，这题不用 Kruscal 重构树也能做。先不看强制在线，那么显然就是对海拔从大到小排序，用并查集，在这个并查集里维护最小 $d_x$，每次海拔达到就新增一条边。那么强制在线后，直接可持久化就行。

CF1628E Groceries in Meteor Town

给出树，点有黑白色，边有边权。

多次询问，将区间 $[l,r]$ 变成黑/白。询问 $u$ 到达不包含本身的边权最大值。

把这棵树变成 Kruscal 重构树。

然后一次询问，就相当于找一个深度最小的虚点，使其为 $u$ 与一个白点的 LCA。

有一个经典性质：一个点集的 LCA 为 dfs 序最小者与最大者 LCA。用线段树维护即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

while (q --) {
    int opt, l, r;
    scanf ("%d", &opt);
    if (opt <= 2) {
        scanf ("%d%d", &l, &r);
        sgt.modify (1, 1, n, l, r, (opt - 1));
    } else {
        scanf ("%d", &l);
        int L = sgt.t[1], R = sgt.tmx[1];
        if ((L == R && id[L] == l) || L == N) puts ("-1");
        else                                  printf ("%d\n", max (w[lca (id[L], l)], w[lca (id[R], l)]));
    }
}

struct SegmenTree { 
    int t[N << 2], tmx[N << 2], rmn[N << 2], rmx[N << 2], lzy[N << 2];
    #define ls (u << 1)
    #define rs (u << 1 | 1)
    #define mid (l + r >> 1)

    void upd (int u, int col) { lzy[u] = col; if (col) t[u] = N, tmx[u] = -N; else t[u] = rmn[u], tmx[u] = rmx[u]; }
    void pushup (int u) { t[u] = min (t[ls], t[rs]); tmx[u] = max (tmx[ls], tmx[rs]); }
    void pushdown (int u) { int& p = lzy[u]; if (p != N) upd (ls, p), upd (rs, p), p = N; }
    
    void build (int u, int l, int r) {
        rmn[u] = t[u] = lzy[u] = N; rmx[u] = tmx[u] = -N;
        if (l == r) return rmn[u] = rmx[u] = dfn[l], void ();
        build (ls, l, mid), build (rs, mid + 1, r);
        rmx[u] = max (rmx[ls], rmx[rs]);
        rmn[u] = min (rmn[ls], rmn[rs]);
    }

    void modify (int u, int l, int r, int ql, int qr, int k) {
        if (l >= ql && r <= qr) return upd (u, k);
        pushdown (u);
        if (ql <= mid) modify (ls, l, mid, ql, qr, k);
        if (qr >  mid) modify (rs, mid + 1, r, ql, qr, k);
        pushup (u); //fprintf (stderr, "now [%d, %d] max = %d, min = %d\n", l, r, tmx[u], t[u]);
    }
} sgt;

3. 连通性问题

3.1 强连通分量

3.1.0、有向图的 DFS 生成树

(1) DFS 序

$u$ 的 DFS 序即为从某节点（根）开始遍历，首次到达 $u$ 的时间戳。

(2) 四条边

1. 树边：DFS 树上的边。
2. 返祖边：指向祖先节点的边。
3. 前向边：指向子孙节点的边。
4. 横叉边：指向的访问过的节点既不是自己的祖先节点也不是自己的子孙。

如下图，黑边为树边，绿边为返祖边，粉边为前向边，红边为横叉边。

图 $G$

$G$ 的 DFS 生成树

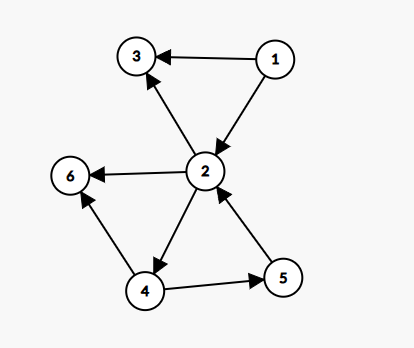
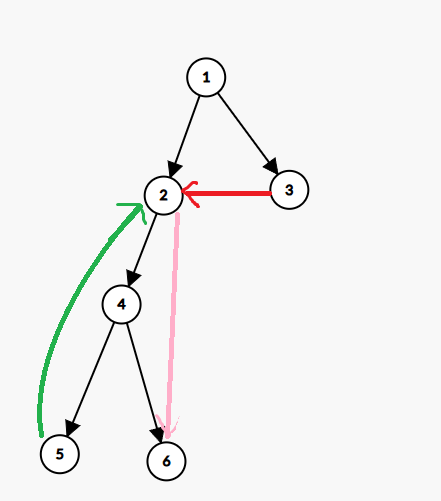
• 强连通：在有向图 $G$ 中，任意两点联通。

• 强连通分量（SCC）：有向图 $G$ 中，极大的强连通子图。对于“极大”，意思是这个子图无法再加入任意一点使其仍为强连通的。

• SCC 的根：遍历这个 SCC 的第一个点

• $dfn_u$：遍历到 $u$ 的时间戳。

• $low_u$：以 $u$ 为根的子树可以回溯到最早已经在栈中的节点的时间戳。

3.1.2 算法过程

我们于 dfs 过程中维护一个栈，里面是未处理的节点。

对于 $u$，我们枚举每一条 $u$ 出边 $(u,v)$。

• 若 $v$ 未访问。我们向 $v$ 遍历，并更新 $low_u\gets\min(low_u,low_v)$。
• 若 $v$ 已访问，且在栈内。$low_u\gets\min(low_u,dfn_v)$。
• 若 $v$ 已访问，不在栈内。那么 $v$ 所在 SCC 已经处理完毕，不操作。

值得注意的是，有时在写强连通分量时，我们误将 $low_u\gets\min(low_u,dfn_v)$ 写作 $low_u\gets\min(low_u,low_v)$，虽然运行结果正确。然而这实际上不符合我们推导以及思考过程，在求双连通分量中这样是错误的。因此需要注意这个问题。

对于一个 SCC，有且仅有一个点使得 $low_u=dfn_u$。

我们只需找到这样的点，将这个点以及栈内所有晚于这个点入栈的点弹出，所构成的即为一个 SCC。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

void tarjan (int x) {
    dfn[x] = low[x] = ++ tim;
    inst[x] = true;
    st.push (x);

    for (auto to : e[x]) {
        if (!dfn[to]) tarjan (to), low[x] = min (low[x], low[to]);
        else if (inst[to]) low[x] = min (low[x], dfn[to]);
    }

    if (dfn[x] == low[x]) {
        int tp;
        ans.push_back ({});
        do {
            tp = st.top (); st.pop ();
            ans.back ().push_back (tp);
            id[tp] = ans.size ();
            inst[tp] = false;
        } while (tp != x);
    }
}

这整个过程的时间复杂度非常优秀，为 $\mathcal O(n+m)$。

3.1.3 例题

P3387 【模板】缩点

模板题。 我们可以发现，在经过缩点操作后的新图是一个有向无环图，故可以在新图上进行 DP 操作。

P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G

对原图缩点后，原图中属于出度为 $0$ 的那个点的所有点即为答案。

P2812 校园网络【[USACO]Network of Schools加强版】

缩点，第一个答案为新图入度为 $0$ 点的个数，第二个答案为入度为 $0$ 点个数与出度为 $0$ 点个数的最大值。

P4306 [JSOI2010] 连通数

缩点后建反图，拓扑 DP 即可。 另解：用 bitset 优化的传递闭包。

P2272 [ZJOI2007] 最大半连通子图

原图上是存在环的，所以我们先缩点，得到一张 DAG。根据半连通的定义，我们从入度为 $0$ 的点开始 DP。设 $c_i$ 表示 SCC $i$ 所含节点数，$f_i$ 表示到 $i$ 的最大半连通子图节点数，$g_i$ 表示方案数。那么对于边 $(u,v)$，$f_v\gets \max(f_v,f_u+c_v)$，$g_v\gets\begin{cases}g_u,& f_v<f_u+c_v\\g_u+g_v,&f_v=f_u+c_i\end{cases}$。

3.1-ex 2-SAT 问题

3.1-ex.1 简介

给出 $n$ 个布尔 $x_1,x_2\cdots,x_n$ 以及 $m$ 条限制。每条限制形如「$x_i$ 为真/假 或 $x_j$ 为真/假」。请对这 $n$ 个布尔进行赋值，使得 $m$ 条限制都满足。

考虑建立大小为 $2n$ 的图，对于 $x_i$ 以及 $\neg x_i$ 都建立一个点。对于一个限制 $x_i \or x_j$，建边 $\neg x_i\to x_j$ 以及 $\neg x_j\to x_i$，表示「若其一不满足，则另一必满足」。之后对整张图跑强连通分量。

对于属于同一强连通分量的点，条件等价，即可以互推。若 $x_i$ 与 $\neg x_i$ 同属同一个强连通分量，那么说明无解。

对于有解情况，我们对新图跑拓扑排序。若 $\neg x_i$ 的拓扑序在 $x_i$ 之前，那么显然 $x_i=\mathrm{True}$，否则若 $x_i=\mathrm{False}$，那么 $\mathrm{True}\to \mathrm{False}$，假。因此 $x_i=\mathrm{True}$。

在逻辑上，蕴含关系定义为：$p\to q\equiv \neg p\or q$。

当 $p$ 蕴含 $q$ 时，任意的真 $p$ 必然可以推出 $q$。而当「 $p$ 成立且 $q$ 不成立」这个命题成立时，这个命题为假。这等价于「$p$ 不成立或者 $q$ 成立」不成立，即 $\neg p\or q =\mathrm{False}$ 时，这个命题为假。相应的，当 $\neg p\or q=\mathrm{True}$ 时，$p\to q$ 为真。根据这一点，我们有真值表：

$p$	$q$	$p\to q$
T	T	T
T	F	F
F	T	T
F	F	T

这就解释了 2-SAT 问题的解法。

3.1-ex.2 例题

P3825 [NOI2017] 游戏

有三个场地：A, B, C。

每个点有限制，为不能选 ABC 其一，或者都能选。

给出 $m$ 个条件：$(i,h_i,j,h_j)$ 表示若 $i$ 选 $h_i$ 则 $j$ 选 $h_j$。

构造一种方案，使得满足所有条件以及限制。

$n\le 5\times10^4,m\le 10^5$。满足都能选的点不超过 $8$ 个。

先不看都能选的，假设限制都是不能选其一。假设不能选 $C$，设布尔变量 $x_i=0/1$ 表示 $i$ 点选 A/B。对于一组条件 $(i,h_i,j,h_j)$ 相当于 $x_i=h_i\to x_j=h_j$。连边 $x_i= h_i\to x_j=h_j$ 以及 $x_j=\neg h_j\to x_i= \neg h_i$，这就是一个 2-SAT 问题。

对于剩下都可选的点，不妨对其进行分配，分别假设为不能为 A/B（这两种分别可能为 BC/AB，包含所有情况，所以不用假设为 C），然后建边跑 2-SAT，时间复杂度为 $\mathcal O(2^d(n+m))$。

注意一种情况：当 $h_j=s_j$ 时，$i$ 一定不能选 $h_i$。假设 $h_i$ 为 $x_i$，那么这个条件可以直接连边 $x_i\to\neg x_i$ 表示。存边时不要分开存，否则会出现意想不到的错误。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

int main (void) {

    cor['a'][0] = 'B', cor['a'][1] = 'C'; bul['a']['B'] = 0; bul['a']['C'] = 1;
    cor['b'][0] = 'A', cor['b'][1] = 'C'; bul['b']['A'] = 0; bul['b']['C'] = 1;
    cor['c'][0] = 'A', cor['c'][1] = 'B'; bul['c']['A'] = 0; bul['c']['B'] = 1;
    scanf ("%d%d", &n, &d); scanf ("%s", s + 1); sg.assign (N, {}); 
    int m; scanf ("%d", &m);
    for (int i = 1; i <= m; i ++) {
        int u, v; char s1[5], s2[5];
        scanf ("%d%s%d%s", &u, s1 + 1, &v, s2 + 1);
        limit.push_back ({u, s1[1], v, s2[1]});
    }

    for (int i = 0; i < (1 << d); i ++) {

        int cnt = 0;
        strcpy (t + 1, s + 1);
        g = sg; color = tim = tp = 0; 
        for (int j = 1; j <= n; j ++) if (t[j] == 'x') t[j] = 'a' + (i >> cnt & 1), ++ cnt;
        for (auto& [u, s1, v, s2] : limit) {
            if (s1 == t[u] - 32) continue;
            if (s2 == t[v] - 32) {
                g[ u + n * bul[ t[u] ][ s1 ] ].push_back (u + n * (1 ^ bul[ t[u] ][ s1 ]));
                continue;
            }
            g[ u + n * bul[ t[u] ][ s1 ] ].push_back (v + n * bul[ t[v] ][ s2 ]),
            g[ v + n * (bul[ t[v] ][ s2 ] ^ 1) ].push_back (u + n * (bul[ t[u] ][ s1 ] ^ 1));
        }
                                        
        for (int i = 1; i <= n << 1; i ++) dfn[i] = low[i] = 0;
        for (int i = 1; i <= n << 1; i ++) if (!dfn[i]) tarjan (i);
        bool flag = true;
        
        for (int i = 1; i <= n; i ++) if (col[i] == col[i + n]) { flag = false; break; }
        if (!flag) continue;
        for (int i = 1; i <= n; i ++) putchar (cor[t[i]][col[i] > col[i + n]]);
        return puts (""), 0;
    }

    puts ("-1");
    
    return 0;
}

P6378 [PA 2010] Riddle

给出 $n$ 点 $m$ 边的无向图，这 $n$ 个点被分成 $k$ 部分。选一些关键点，使每部分仅有一个关键点，每条边左右至少有一个关键点。

对于一条边 $(u,v)$ 的限制，即为条件 $\neg u\to v,\neg v\to u$。对于关键点的性质，如果直接暴力建图，显然行不通。考虑前后缀优化建图。对于一部分建前后缀点。设 $pre_i$ 表示前缀 $[1,i]$ 中存在关键点。那么对于点 $a_i$，连边：

$$a_i\to \neg pre_{i-1},pre_{i-1}\to\neg a_i\\pre_{i-1}\to pre_i,\neg pre_{i}\to\neg pre_i\\a_i\to pre_i,\neg pre_i\to\neg a_i$$

最后跑 2-SAT 即可。

3.2 双联通分量，割点与桥

3.2-ex 圆方树与仙人掌

3.3 DAG 连通性

记 $f_{i,j}$ 表示 $i$ 是否能到达 $j$，将所有点拓扑排序，将所有出边用 bitset 维护或即可。时间复杂度 $\mathcal O(\dfrac {nm}\omega)$。

3.3. 例题

[P11369 [Ynoi2024] 弥留之国的爱丽丝

如果对于每次查询都跑一次 DAG 可达性，$\mathcal O(\dfrac{nmq}\omega)$，显然无法接受。考虑操作分块。

假设块长为 $B$，设 $b_i$ 为第 $i$ 个块。对于块 $b_i$，我们设 $b_i$ 中修改操作中的边为「关键边」，关键边的点以及所有询问的点为「关键点」。对于所有非关键边、关键点的点，且不含非黑边的图做一次缩点，得到一个 DAG。我们在这个 DAG 上预处理出所有 $f_{i,j}=1/0$ 表示关键点 $i$ 是否可以到达关键点 $j$。显然关键点的数量是 $O(B)$ 的，那么我们对于块内每次查询，对于 $f$ 跑一次类 DAG 可达性即可。

?. 杂项

.1 定长路径计数

.1.1 基础：AtCoder DP R

给出邻接矩阵，$G_{ij}=1/0$ 表示存在/不存在边 $i\to j$，求长度为 $K$ 的路径数。

考虑 DP。$f(i,j)$ 表示长度为 $i$ 终点为 $j$ 的路径总数。那么有 $f(i,j)=\sum\limits_{u=1}^n G(u,j)\times f(i-1,u)$。降维，即 $f(j)=\sum\limits_{u=1}^n G(u,j)\times f_{last}(u)$，这和矩阵乘法的形式不谋而合。那么 $f_{ans}=G^K f_0$，$f_0$ 初始为长度为 $n$ 的列向量，全为 $1$。

code

.1.2 进阶：P4159 [SCOI2009] 迷路

给出邻接矩阵，边有小于 $10$ 的权，求 $1\to n$ 有多少路径。

拆点，把路径拆成边权为 $1$ 多个点的路径，然后矩阵快速幂即可。

code

.1.3 进阶 2：P2151 [SDOI2009] HH 去散步

给出 $m\le60$ 条 无向边，不能 连续 经过一条边。求 $s\to e$ 的路径数。

难以维护点矩阵做。考虑转化为 边矩阵 解决。我们只需将原图关系映射到一个由边组成的矩阵上即可实现。下面用链式前向星说明构造方法。

设 $cnt=0$，我们先加入 $0\to s$ 这条边，这是这是题设的一部分。后每次加入一条无向边 $u\to v$，编号相邻，且互为与 $1$ 异或值。我们在构造矩阵时，只需使 $i\not=j\operatorname{XOR} 1$ 就令 $G_{ij}=1$。接下来操作同上。答案为 $\sum\limits_{to_j=e}G_{1j} $。

code

基环树

https://www.luogu.com.cn/article/0i6swvk6

三元环计数

欧拉图

• 欧拉路径：能够经过所有边恰好一次的连通图。
• 欧拉回路：能够经过所有边恰好一次并回到起点的连通图。
• 欧拉图：存在欧拉回路。
• 半欧拉图：存在欧拉路径但不存在欧拉回路。

欧拉图的判定

有向欧拉图的判断法则：$G$ 为弱连通且任意一点出度与入度相同。 有向半欧拉图的判断法则：$G$ 弱连通，存在两点恰为出度 $+1$ 与 $-1$，其余点出入度均相等。

无向欧拉图的判断法则：$G$ 连通且每个点的度数均为偶数。 无向欧拉图的判断法则：$G$ 连通且 恰存在 两个点的度数为奇数。

Hierholzer 求欧拉回路

说一下具体做法吧，不做证明。首先，找到一个出度大于入度的点 $u$ 作为起点（不存在则为欧拉回路，任意点作为起点），从 $u$ 点开始 dfs。dfs 时遍历每条没有访问过的边，并注意采用当前弧优化。注意判断是否有解。时间复杂度 $\mathcal O(n+m)$。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

int n, m, idg[N], odg[N], hd[N];
vector <int> g[N];
int ans[N], top;

void dfs (int u) {
    for (int& i = hd[u]; i < g[u].size (); ) dfs (g[u][i ++]);
    ans[++ top] = u;
}

int main (void) {

    scanf ("%d%d", &n, &m);
    for (int i = 1, u, v; i <= m; i ++) scanf ("%d%d", &u, &v), g[u].push_back (v), idg[v] ++, odg[u] ++;

    bool flag1 = false; int st = -1;
    for (int i = 1; i <= n; i ++) {
        if (odg[i] > idg[i]) {
            if (flag1) return puts ("No"), 0;
            st = i;
            flag1 = true;
        }
        sort (g[i].begin (), g[i].end ());
    }

    dfs (st == -1 ? 1 : st);

    if (top != m + 1) return puts ("No"), 0;

    for (int i = top; i; i --) printf ("%d ", ans[i]);

    return 0;
}

例题

P11762 [IAMOI R1] 走亲访友

下文中 $K$ 表示我们需要走的路径条数。

• $K\le 2m$ 做法：在 dfs 生成树的所有返祖边走两遍，第二遍删掉即可。
• $K\le n + m$ 做法：若将原图补成一个欧拉回路，那方案就是删除所有非生成树边。我们在 dfs 生成树上，若 $u$ 度数为奇，那么将 $u$ 与 $fa_u$ 连一条边，可以递归地证明这样做最终会形成欧拉回路的。这样，我们最多加了 $n-1$ 条边，因此我们生成的路径至多有 $n+m-1$ 条。时间复杂度 $\mathcal O(n+m)$。

注意细节，当前弧优化非常重要。

code

CF547D Mike and Fish

转化：把每一列与每一行当做图中一个点，那么给出的平面上点 $(x_i,y_i)$ 即为图上一条边。

点的颜色可以视作 边的指向。具体来说，每个平面点具有红蓝两种属性，而边也有出入两种属性，因此这样是可以一一对应的。那么问题也就转化为了每个点的出入度之差不超过 $1$。欧拉回路是满足这个条件的一个图。那么我们只需要在转化后的图上跑欧拉回路即可。What’s more，若存在奇点，那么设 $0$ 虚点与其向连即可。

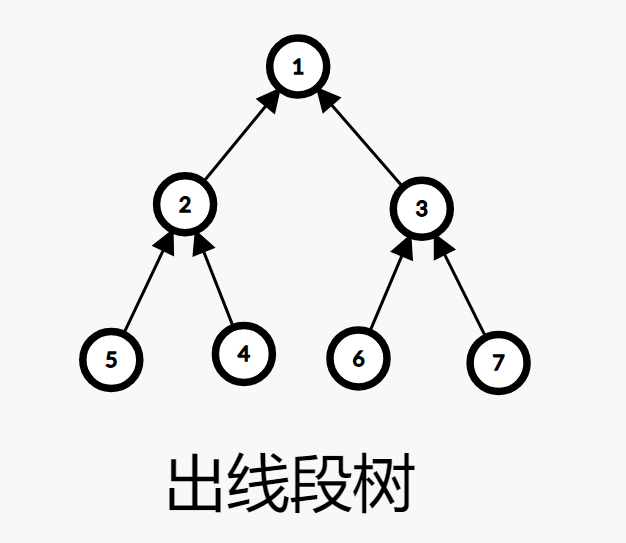
优化建图

线段树优化建图

适用于形如「区间 $[l_1,r_1]$ 的点」向「区间 $[l_2,r_2]$ 的点」连边的建图。

我们建两棵线段树，一棵为「入线段树」，一棵叫「出线段树」。每次增加 $[l_1,r_1]\to [l_2,r_2]$ 的边时，新建虚点 $P$。将 $[l_1,r_1]$ 拆分成出线段树上的 $\mathcal O(\log n)$ 个节点后，向 $P$ 连边。再从 $P$ 向 $[l_2,r_2]$ 被拆分成入线段树的 $\mathcal O(\log n)$ 个节点连边。

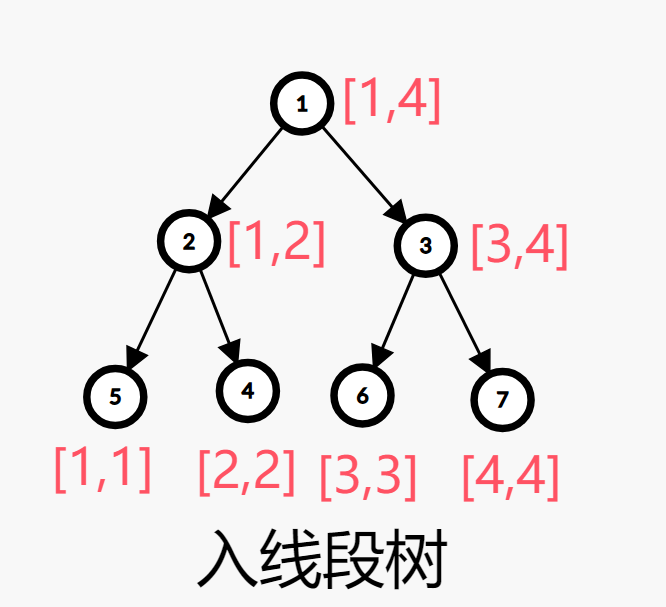
CF786B Legacy

模板题。

注意的一点是，每个点的入点向出点连边（跟网络流的思想差不多）。

Submission

前后缀优化建图

可以对于每个前/后缀都建一个虚点。假设前缀虚点 $p_i$ 表示连 $[1,i]$ 中的点，那么实际上只要连 $p_i\to p_{i-1}$ 以及 $p_i\to i$ 即可。同样的，这也需要考虑出点与入点的问题。

堆优化存边

好玩题

P1084 [NOIP 2012 提高组] 疫情控制

给出 $n\le 5\times10^4$ 个节点的有边权的树，有 $m$ 个人，在节点上。

每个人可以花费边权时间移动，不能移到根，可以同时。求最小时间（即移动时间最大值），使得每个叶子结点的祖先至少有一个人。

这个答案显然具有单调性，因此考虑二分，问题转化为判断一段时间内是否能使每个叶子节点被管辖。显然，每个叶子节点被管辖，当且仅当有人在其到根的链（不含根）上。我们称每个叶子结点所在链的顶为其「类别」，链顶与根节点的边权为「权」。

一个显然的观察是：每个人往上跳的越远越优。接下来考虑跨越根节点的情况。

把根的子节点有人的都拿出来，把剩下的「可用时间」从大到小入队。找到所有没有被完全管辖的「类别」，按照「权」从大到小入队。这样就可以贪心的计算。

另外，对于当前「类别」顶没匹配完的，尽量匹配当前类别。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

bool bfscheck (const vector <int>& times, vector <int>& vis, int u) {
    if (g[u].size () == 1) return times[u] > 0;
    vector <int> tmp; tmp.push_back (u);
    
    while (!tmp.empty ()) {
        int u = tmp.back (); tmp.pop_back ();
        if (times[u]) break;
        for (const auto& [v, w] : g[u]) {
            if (g[v].size () == 1) return false;
            if (fa[v][0] == u && !vis[v]) tmp.push_back (v);
        }
    }
    return true;
}

bool check (ll tot_time) {
    vector < pair <int, ll> > st; vector <int> signi; signi.assign (n + 1, 0);
    for (auto u : sig) {
        st.push_back ({u, 0});
        for (int i = 16; ~i; i --)
            if (fa[u][i] > 1 && st.back ().second + cost[u][i] <= tot_time) {
                st.back ().first = fa[u][i];
                st.back ().second += cost[u][i];
                u = fa[u][i];
            }
        signi[st.back ().first] ++;
    } // jump 
    vector <int> vis; vis.assign (n + 1, 0);
    vector <int> q; for (const auto& [u, w] : st) q.push_back (u);
    while (!q.empty ()) {
        int u = q.back (); q.pop_back ();
        vis[u] = true;
        for (const auto& [v, w] : g[u]) 
            if (fa[v][0] == u && !vis[v]) q.push_back (v), vis[v] = true; 
    } // find trees without SIG points 
    vector <int> unac; 
    for (const auto& lef : leaf) if (!vis[lef]) unac.push_back (typ[lef]);
    vis.assign (n + 1, 0);

    sort (st.begin (), st.end (), [&](auto x, auto y) { return x.second < y.second; });
    vector < pair <ll, int> > avail; vector <int> usin; usin.assign (n + 1, 0);
    for (const auto& [u, w] : st) {
        if (fa[u][0] == 1) {
            usin[u] ++;
            -- signi[u]; avail.push_back ({tot_time - w - cost[u][0], u});
            if (!signi[u] && !bfscheck (signi, vis, u)) unac.push_back (u);
        }
    }
    sort (unac.begin (), unac.end (), [&](const auto x, const auto y) { return cost[x][0] > cost[y][0]; }); 
    unac.erase (unique (unac.begin (), unac.end ()), unac.end ()); 
    sort (avail.begin (), avail.end ());
    for (const auto& u : unac) {
        while (avail.size () && !usin[avail.back ().second]) avail.pop_back (); 
        if (avail.empty ()) return false;
        if (cost[u][0] > avail.back ().first && !usin[u]) return false;
        if (usin[u] > 0) usin[u] --;
        else    usin[avail.back ().second] --, avail.pop_back ();
    } 
    return true;
}