DP 优化 I

2025-04-10T19:44:00+08:00 | 8分钟阅读 | 更新于 2025-04-10T19:44:00+08:00

@ Jason Chan

远古时期啦，那时候没钱买正版。但是网易的 Hypixel 玩的很开心，可惜停服了。买了正版玩了一段时间，可惜初中后就不太感兴趣了。却再也找不回。

线段树、单调队列、斜率优化。

线段树优化

我们已经接触过了许多动态规划的类型, 可以使一个问题在多项式复杂度如 $\mathcal O(n^3)$, $\mathcal O(n^2)$ 求解. 但是有时 $n$ 上限会达到 $10^5$ 甚至 $10^6$, 此时这种复杂度就显得过于拙劣了. 那么有没有有一种方法能优化复杂度呢？

考虑形如 $f(i)=\max\limits_{j=1}^{i-1}{g(f(j))}+h(i)$ 的转移方程, 若以朴素算法转移, 那么时间复杂度会达到 $\mathcal O(n^2)$. 但是我们注意到, 这个式子实际上在查询一段区间的最值, 于是自然可以引入数据结构, 线段树是一种处理区间问题的数据结构.

我们只需要定义线段树节点 $c[l,r]$ 表示区间 $[l,r]$ 的最大 $g(f(j))$, 即可以 $\log n$ 的复杂度进行转移. 线段树优化 DP 的思想大致如此.

模板: CF115F Linear Kingdom Races

有 $n$ 条路可以修, 修第 $i$ 条路的花费是 $w_i$. 有 $k$ 个活动, 第 $i$ 个活动由三元组 $[l_i,r_i,p_i]$ 表示, 指若修了 $[l_i,r_i]$ 内所有路则有收益 $p_i$. 求最大收益.

Solution: 设 $f(i)$ 表示前 $i$ 条路的最大值. 若第 $i$ 条不修, 答案为 $f(i)$. 若修, 则枚举从哪个位置修. 故 $f(i)=\begin{cases}f(i-1),\\max{f(j)+val(j+1,i)-cost(j+1,i)\end{cases}$ 可能会对第二个式子有疑惑, 如果越过 $j$ 的收益如何统计? 不必担心, 这种情况会导致答案偏小, 然而我们 $j$ 取遍整个区间, 且取最大值, 故这种情况必定被答案排除在外. 直接 dp 复杂度是 $\mathcal O(n^2)$.

我们现在 dp 的瓶颈是降低第二个式子的复杂度, 我们考虑线段树优化.

由于比赛以 $r$ 结尾才有贡献, 故以 $r$ 偏序, 枚举以 $r$ 结尾的所有比赛. 我们设线段树节点 $c[l,r’]$ 的意义为 $\max\limits_{i=l+1}^{r’}{f(i)+val(i,r)-cost(i,r)}$. 每次枚举到一个新的 $r$ 时, 即需要修新路, 故将 $c[0,r-1]$ 减去 $w_r$. 即 $cost(i,r+1)=cost(i,r)+w_r$. 后枚举可以作出贡献的 $l$, $c[0,l-1]$ 加上贡献 $p$, 即包含区间 $[l,r]$ 的所有区间加上 $p$. 于是, 进行状态转移, $f(r)=\max{f(r-1),c[0,r-1]}$. 最后, $r\gets r+1$, 令 $r’=r+1$, 已求出 $f[r]$, 故将 $c[r,r’]\gets f[r]$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


    scanf ("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf ("%lld", w + i);
    for (int i = 1; i <= m; i ++) {
        ll L, R, P;
        scanf ("%lld%lld%lld", &L, &R, &P);
        range[R].push_back ({L, P});
    }  
 
    for (int R = 1; R <= n; R ++) {
        add (1, 0, n, 0, R - 1, -w[R]);
        for (auto A : range[R]) {
            auto L = A.first, P = A.second;
            add (1, 0, n, 0, L - 1, P);
        }
        dp[R] = max (dp[R - 1], query (1, 0, n, 0, R - 1));
        modify (1, 0, n, R, R, dp[R]);
    }

练习 [NOIP2023] 天天爱打卡

与模板并无区别, 离散化一下即可.

例题 ARC073D Many Moves

长度为 $n$ 整数轴上的两个点 $A,B$ 初始处于 $a,b$, 共 $Q$ 次操作, 每次操作给出 $x_i$, 要求将任意一个点移动到 $x_i$, 移动一个单位长度需要 1s. 求最短时间. $n,Q\le2\times10^5$.

Solution: 设 $f(i,j)$ 操作完前 $i$ 个要求, 表示一个棋子在 $x_i$, 另一个棋子在 $j$ 的最短操作时间. 显然有状态转移式: $$f(i,j)\gets f(i-1,j)+|x_i-x_{i-1}| \ f(i,x_{i-1})\gets\min{f(i-1,j)+|j-x_{i}|}$$

爆空间, 怎么办?

状态优化. 从状态定义中, 我们发现需要根据操作顺序进行 DP, 故将第一维省去, 空间线性.

直接 DP 是 $\mathcal O(nQ)$ 的, 怎么办?

线段树优化. 第一个式子无需优化. 第二个式子可以拆成 $\begin{cases}\min{f(i-1,j)+j}-x_{i}, & j\ge x_i, \ \min{f(i-1,j)-j}+x_{i},&j<x_i\end{cases}$ 对于当前枚举到的 $i$, 我们设 $c_k[l,r]$ 表示 $\min\limits_{j=1}^n{f(i-1,j)-j\times(-1)^{k}}$, 则上式即可化为 $\min{c_0[x_i,n],c_1[1,x_i]}$. 于是复杂度就变成了 $\mathcal O(Q\log n)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


    scanf ("%d%d%d%d", &n, &q, &a, &b); SMT :: build (1, 1, n); x[0] = a; 
    SMT :: modify (1, b, b, 0);
    for (int i = 1; i <= q; i ++) {
        scanf ("%d", x + i);
        ll fir = SMT :: query (1, x[i], n, 1) - x[i]; // query 的第四个元素指哪一个线段树.
        ll sec = SMT :: query (1, 1, x[i], 0) + x[i];
        SMT :: add (1, 1, n, abs (x[i] - x[i - 1]));
        SMT :: modify (1, x[i - 1], x[i - 1], min (fir, sec));
    }   

    printf ("%lld\n", SMT :: query (1, 1, n, 2));

单调队列优化

形如 $f(i)=\min/\max {f(j)+A(i)+B(j)}$ 的式子，其中 $A(i)$ 是关于 $i$ 的函数，$B(j)$ 是关于 $j$ 的函数。我们将 $A(i)$ 分离出来，式子变为 $f(i)=\min/\max {f(j)+B(j)}+A(i)$，对 $f(j)+B(j)$ 进行单调维护，即可将原 $\mathcal O(n^2)$ 的复杂度降到 $\mathcal O(n)$。

P1886 滑动窗口 /【模板】单调队列

给出一段 $n$ 的序列，求每个长度为 $k$ 的子段中元素的最大值。$n\le 10^6$。

以元素大小为第一关键字，构成单调队列。每次的队头即为答案。

代码以前写的太丑陋了，看下面例题的吧。

P3572 [POI 2014] PTA-Little Bird

$n$ 棵树，第 $i$ 树树高为 $d_i$。从第 $1$ 棵开始，每次可以从第 $i$ 棵飞到第 $j\in[i+1,i+k]$ 棵。若 $d_j\ge d_i$，则劳累值加 $1$。求飞到第 $n$ 棵树的最小劳累值。$n\le 10^6$。

设 $f(i)$ 表示飞到第 $i$ 棵的最小劳累值，则 $f(i)=\min\limits_{j\in[i-k,i)}{f(j)+[d_j\ge d_i]}$。时间复杂度 $\mathcal O(n^2)$，爆了。

注意到每次增加值至多为 $1$，那么可以想到用单调队列维护。比较第一关键字是 $f(i)$ 大小，第二关键字是 $d_i$ 大小。每次 dp 直接选队头元素进行比较即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


memset (f, 0x3f, sizeof f);
f[1] = 0; int l = 1, r = 0;
q[++ r] = 1;
for (int i = 2; i <= n; i ++) {
	while (l <= r && i - q[l] > k) l ++;
	f[i] = f[ q[l] ] + (d[i] >= d[ q[l] ]);
	while (l <= r && (f[i] < f[ q[r] ] || f[ q[r] ] == f[i] && d[i] >= d[ q[r] ])) r --;
	q[++ r] = i;
}
printf ("%d\n", f[n]);

斜率优化

对于形如 $F(i)=\min/\max{F(j)+A(i)+B(j)+A(i)B(j)}$ 且满足 $A(i)$ 单调增的状态转移式，可以进行 斜率优化 来降低复杂度。通过下面这道 经典例题 来入门。

P3195 [HNOI2008] 玩具装箱

设 $S_i=\sum\limits_{j=1}^iC_i$，$F(i)$ 表示答案。$F(i)=\min{F(j)+(S_i+i-S_j-j-L-1)^2}$，设 $A(i)=S_i+i$，$B(j)=S_j+j+L+1$。 $\begin{aligned}F(i)&=F(j)+(A(i)-B(i))^2 \ &=F(j)+A(i)^2+B(j)^2-2A(i)B(j) \ &=F(j)+B(j)^2-2A(i)B(j)+A(i)^2 \end{aligned}$ 即 $F(j)+B(j)^2=2A(i)B(j)+F(i)-A(i)^2$。

我们令 $Y(j)=F(j)+B(j)^2$，$k=2A(i)$，$X(j)=B(j)$，$b=F(i)-A(i)^2$。则上式即为 $Y(j)=k\cdot X(j)+b$，呈直线的点斜式。

对于所有的 $j$，构成多个点 $(B(j),F(j)+B(j)^2)$。由于 $A(i)^2$ 是定值，$b=F(i)-A(i)^2$。故截距 $b$ 越小，$F(i)$ 就越小。我们只需找到依次过所有点的直线中，截距最小的，即可求得 $F(i)$。

一个斜率介于 $BC$ 与 $CD$ 之间的直线

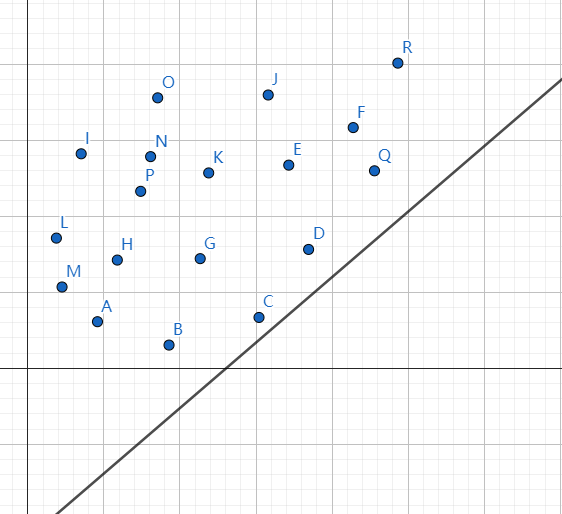
我们以这张图为例，这条直线的斜率介于 $BC$ 和 $CD$ 之间，那么我们向上平移这条直线，显然最先触碰到 $C$ 点。那么 $C$ 点就是这条直线的最优解。

也就是说，我们取 $C$ 点的 $j$ 值，这个 $j$ 就是这个斜率为 $k=2A(i)$ 直线即 $F(i)$ 的最优策略。直接转移即可得到 $F(i)$。

这条直线可以介于许多对线段斜率之间，然而为了使截距最小，我们选择的点必须在这所有点的外围，也就是这些点的凸包上。由于直线的斜率 $k=2A(i)$ 是单调增的，因此可以考虑使用 单调队列 维护所有点，这也与上一个优化方式不谋而合。

问题也便转化为了如何动态维护凸包。不妨假设已经维护了 $k$ 个点的凸包，那么如何处理新增点？

有 $k$ 个点的凸包

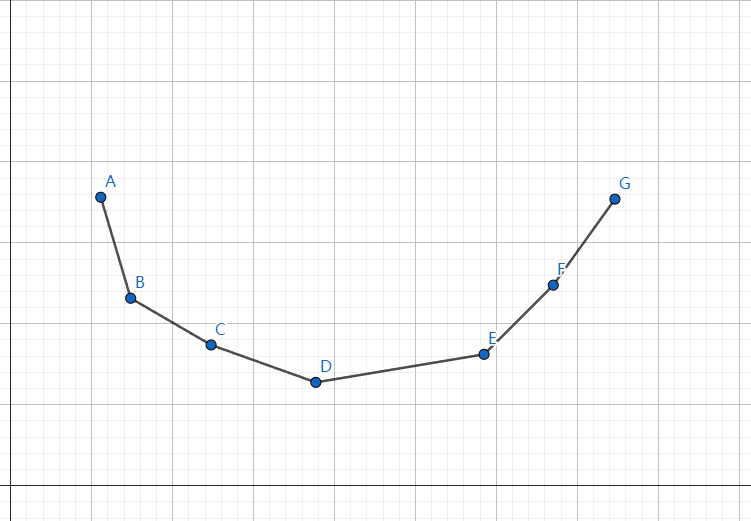
我们很容易发现凸包上相邻两点连线的斜率是不断递增的，于是可以做出以下分类讨论：假设新增点为 $P$。

如若 $k_{PG}\ge k_{FG}$，那么直接入队即可。
如若 $k_{PG}<k_{FG}$，那么需要一直从队尾出队，直至 $P$ 与队尾点的斜率不小于上一个点与队尾点的斜率。

$k_{GP}$ 与 $k_{FP}$ 均不满足单调增的处理

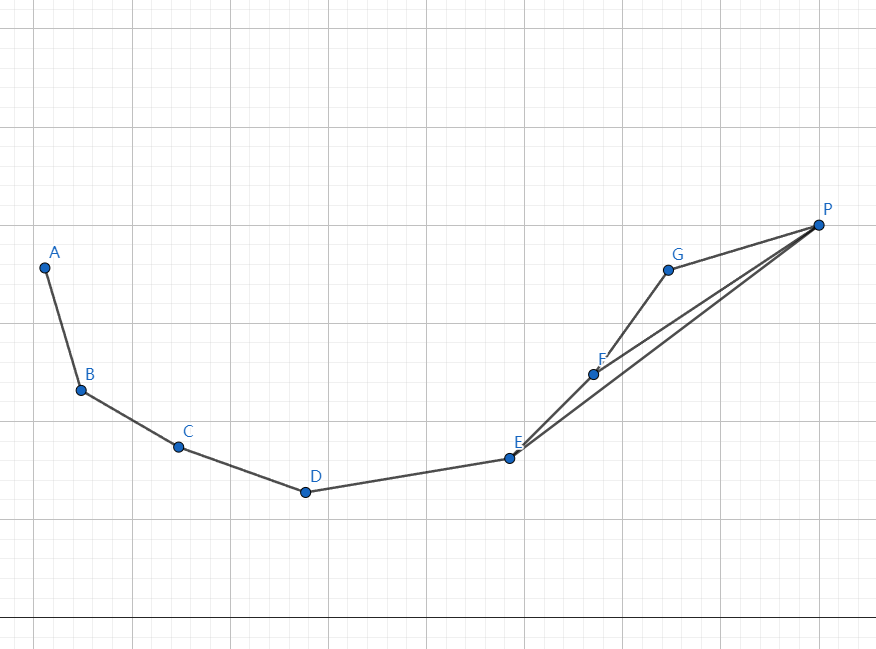
那么如若新增的 $P$ 点在 $G$ 点左侧，怎么办？

$P$ 点在 $G$ 点左侧的示例

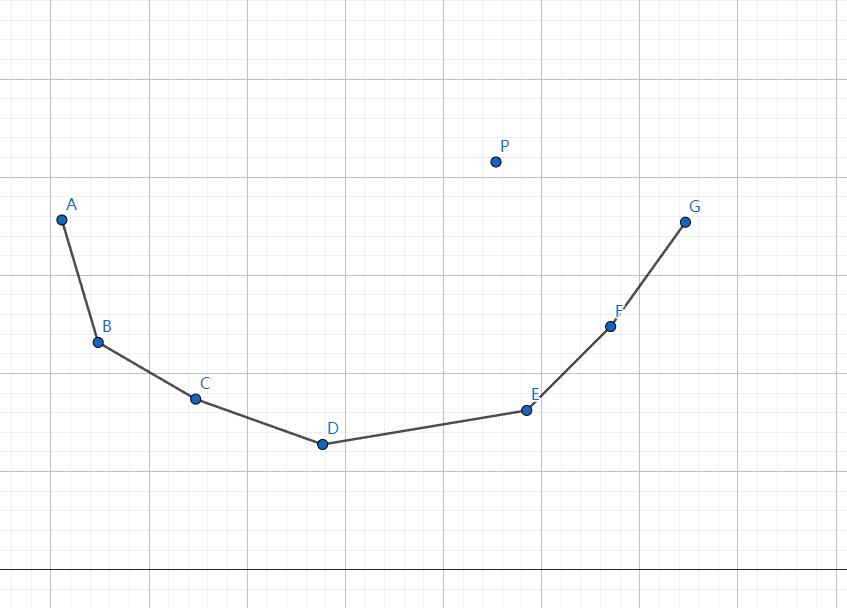
很简单，不入队即可。而且由于本题的 $X(j)=S_j+L+1+j$，即每个点的横坐标是递增的，因此无需考虑这种情况。其实到这里已经可以发现，我们实际上维护的是并非完整的凸包，而是凸包的 下凸壳，这是因为我们需要求得截距的 最小值，并非每道斜率优化的题目都必须维护下凸壳，例如求截距最大值便是维护上凸壳。

如此，我们基本上已经了解了斜率优化的所有步骤，总结一下如下：

从队头开始，若队头与其相邻点连成线段的斜率小于 $k=2A(i)$，出队；
那么队头就为所说的最优解，取队头点进行状态转移；
删除队尾点直至使相邻斜率单调增，后加入当前点 $(X(i),Y(i))$。

值得注意的是，至少有两个点才能进行斜率计算，如若没有两个点，那么无需操作。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


#include <cmath>
#include <iostream>

#define ll long long

using namespace std;

const int MAXN = 5e4 + 10;

int n, l;
ll s[MAXN], A[MAXN], B[MAXN], dp[MAXN], q[MAXN];

ll sq (ll x) { return x * x; }
ll X (int i) { return B[i]; }
ll Y (int i) { return dp[i] + sq (B[i]); }
double slope (int i, int j) { return (double)(Y (i) - Y (j)) / (X(i) - X(j)); } 

int main (void) {

    scanf ("%d%d", &n, &l); l ++;
    for (int i = 1; i <= n; i ++) scanf ("%lld", s + i), s[i] += s[i - 1], A[i] = s[i] + i, B[i] = s[i] + i + l;
    B[0] = l;
    int l = 1, r = 0; q[++ r] = 0;
    for (int i = 1; i <= n; i ++) {
        while (l < r && slope (q[l], q[l + 1]) < 2 * A[i] ) ++ l; 
        dp[i] = dp[ q[l] ] + sq ((A[i] - B[ q[l] ]));
        while (l < r && slope (i, q[r]) < slope (q[r - 1], q[r])) -- r;
        q[++ r] = i;
    }

    printf ("%lld\n", dp[n]);

    return 0;
}

为什么要先入队一个 $0$?
如若不入队，则第一个点必不会被删除，违反了上述原则。

P2120 [ZJOI2007] 仓库建设

有 $n$ 个仓库，第 $i$ 个仓库有 $p_i$ 个物品，修建防护的代价为 $c_i$，距离仓库 $1$ 的距离为 $x_i$。每个仓库都可修建防护，且每个物品必须在防护之下。如若 $j$ 仓库不修，那么需要花费 $p_j\times p_k$ 的代价转移到修建防护的 $k$ 仓库（$k>j$）。$n\le 10^6$，求最小代价。

先想到了直接设计状态 $f(i)$：前 $i$ 个仓库的所有物品都处于防护之下的最小代价。然后翻转一下 $x_i,c_i,p_i$，转移式看起来很好写：$f(i)=\min\limits_{j\in[1,i)}{f(j-1)+c_j+\sum\limits_{k=j}^i(x_j-x_k)\cdot p_k}$，然后发现这个式子中涉及了两个量，我做斜率优化时没有成功，这种方法只能有 $\mathcal O(n^2)$ 做法。

于是换个思路，反着 dp。设 $f(i)$：最后一个仓库建在 $f(i)$ 的最优解。转移式也是比较显然的：$f(i)=\min\limits_{j\in[0,i)}{f(j)+c_i+\sum\limits_{k\in[j+1,i]}(x_i-x_k)\cdot p_k}$

然后令 $A(i)=\sum\limits_{k\in[1,i]}x_ip_i$，$B(i)=\sum\limits_{k\in[1,i]}p_i$，那么就是 $f(i)=\min\limits_{j\in[0,i)}{f(j)+c_i+x_i\cdot(B(i)-B(j))-A(i)+A(j)}$。

整理一下，于是 $f(j)+A(j)=x_i\cdot B(j)+(A(i)+f(i)-x_i\cdot B(i)-c_i)$。

维护方法与上题同理。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


#include <iostream>
#include <algorithm>

#define ll long long

using namespace std;

const int MAXN = 1e6 + 10;

int n;
ll x[MAXN], p[MAXN], c[MAXN];
ll A[MAXN], B[MAXN], f[MAXN];
int q[MAXN], l = 1, r = 1;

ll X (int i) { return B[i]; }
ll Y (int i) { return f[i] + A[i]; }
double slope (int i, int j) { ll dY = Y (j) - Y (i); return B[i] == B[j] ? (dY > 0 ? 1e18 : (dY < 0 ? -1e19 : 0)) : (double)dY / (double)(X (j) - X (i)); }

int main (void) {

    scanf ("%d", &n);
    for (int i = 1; i <= n; i ++) {scanf ("%lld%lld%lld", x + i, p + i, c + i);}
    for (int i = 1; i <= n; i ++) A[i] = A[i - 1] + x[i] * p[i], B[i] = B[i - 1] + p[i];

    for (int i = 1; i <= n; i ++) {
        while (l < r && slope (q[l], q[l + 1]) < x[i]) ++ l; int j = q[l];
        f[i] = f[j] + c[i] - ( A[i] - A[j] - x[i] * (B[i] - B[j]) );
        while (l < r && slope (q[r], i) < slope (q[r - 1], q[r])) r --;
        q[++ r] = i;
    }

    ll ans = f[n]; 
    int i = n;  while (i && !(B[i] - B[i - 1])) i --, ans = min (ans, f[i]);

    printf ("%lld\n", ans);

    return 0;
}